有理數
有理數
有理數是“數與代數”領域中的重要內容之一，在現實生活中有廣泛的應用，是繼續學習實數、代數式、方程、不等式、直角坐標系、函數、統計等數學內容以及相關學科知識的基礎。數學上，有理數是一個整數a和一個正整數b的比，例如3/8，通則為a/b。0也是有理數。有理數是整數和分數的集合，整數也可看做是分母為一的分數。有理數的小數部分是有限或為無限循環的數。不是有理數的實數稱為無理數，即無理數的小數部分是無限不循環的數。
有理數集可以用大寫黑正體符號Q代表。但Q並不表示有理數，有理數集與有理數是兩個不同的概念。有理數集是元素為全體有理數的集合，而有理數則為有理數集中的所有元素。
“有理數”這一名稱不免叫人費解，有理數並不比別的數更“有道理”。事實上，這似乎是一個翻譯上的失誤。有理數一詞是從西方傳來，在英語中是rational number，而rational通常的意義是“理性的”。中國在近代翻譯西方科學著作，依據日語中的翻譯方法，以訛傳訛，把它譯成了“有理數”。但是，這個詞來源於古希臘，其英文詞根為ratio，就是比率的意思（這裡的詞根是英語中的，希臘語意義與之相同）。所以這個詞的意義也很顯豁，就是整數的“比”。與之相對，“無理數”就是不能精確表示為兩個整數之比的數，而並非沒有道理。
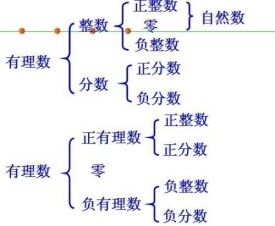
有理數為整數（正整數、0、負整數）和分數的統稱。正整數和正分數合稱為正有理數，負整數和負分數合稱為負有理數。因而有理數集的數可分為正有理數、負有理數和零。由於任何一個整數或分數都可以化為十進位循環小數，反之，每一個十進位循環小數也能化為整數或分數，因此，有理數也可以定義為十進位循環小數。
有理數集是整數集的擴張。在有理數集內，加法、減法、乘法、除法（除數不為零）4種運算通行無阻。
有理數的大小順序的規定：如果 是正有理數，當a 大於或小於b，記作 或。任何兩個不相等的有理數都可以比較大小。
有理數集與整數集的一個重要區別是，有理數集是稠密的，而整數集是密集的。將有理數依大小順序排定后，任何兩個有理數之間必定還存在其他的有理數，這就是稠密性。整數集沒有這一特性，兩個相鄰的整數之間就沒有其他的整數了。
有理數是實數的緊密子集：每個實數都有任意接近的有理數。一個相關的性質是，僅有理數可化為有限連分數。依照它們的序列，有理數具有一個序拓撲。有理數是實數的（稠密）子集，因此它同時具有一個子空間拓撲。
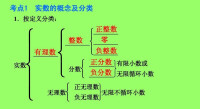
有理數的分類按不同的標準有以下兩種：
（1）按有理數的定義分類：
● ● 同號兩數相加，取與加數相同的符號，並把絕對值相加。
● ● 異號兩數相加，若絕對值相等則互為相反數的兩數和為0；若絕對值不相等，取絕對值較大的加數的符號，並用較大的絕對值減去較小的絕對值。
● ● 互為相反數的兩數相加得0。
● ● 一個數同0相加仍得這個數。
● ● 互為相反數的兩個數，可以先相加。
● ● 符號相同的數可以先相加。
● ● 分母相同的數可以先相加。
● ● 幾個數相加能得整數的可以先相加。
減去一個數，等於加上這個數的相反數，即把有理數的減法利用數的相反數變成加法進行運算。
● ● 同號得正，異號得負，並把絕對值相乘。
● ● 任何數與零相乘，都得零。
● ● 幾個不等於零的數相乘，積的符號由負因數的個數決定，當負因數有奇數個時，積為負，當負因數有偶數個時，積為正。
● ● 幾個數相乘，有一個因數為零，積就為零。
● ● 幾個不等於零的數相乘，首先確定積的符號，然後后把絕對值相乘。
● ● 除以一個不等於零的數，等於乘這個數的倒數。
● ● 兩數相除，同號得正，異號得負，並把絕對值相除。零除以任意一個不等於零的數，都得零。
有理數
零不能做除數和分母。
有理數的除法與乘法是互逆運算。
在做除法運算時，根據同號得正，異號得負的法則先確定符號，再把絕對值相除。若在算式中帶有帶分數，一般先化成假分數進行計算。若不能整除，則除法運算都轉化為乘法運算。
● ● 負數的奇數次冪是負數，負數的偶數次冪是正數。例如：。
● ● 正數的任何次冪都是正數，零的任何正數次冪都是零。例如：
● ● 零的零次冪無意義。
● ● 由於乘方是乘法的特例，因此有理數的乘方運算可以用有理數的乘法運算完成。
● ● 1的任何次冪都是1，-1的偶次冪是1，奇次冪是-1。
加法運算律:
● ● 加法交換律：兩個數相加，交換加數的位置，和不變，即 。
● ● 加法結合律：三個數相加，先把前兩個數相加或者先把后兩個數相加，和不變，即 。
減法運算律：
減法運算律：減去一個數，等於加上這個數的相反數。即： 。
乘法運算律：
● ● 乘法交換律：兩個數相乘，交換因數的位置，積不變，即 。
● ● 乘法結合律：三個數相乘，先把前兩個數先乘，或者先把后兩個相乘，積不變，即 。
● ● 乘法分配律：某個數與兩個數的和相乘等於把這個數分別與這兩個數相乘，再把積相加，即
。
有理數的加減乘除混合運算，如無括弧指出先做什麼運算，按照“先乘除，后加減”的順序進行，如果是同級運算，則按照從左到右的順序依次計算。
在代數運算中不當使用除以零可得出無效證明： 。前提a 不等於b。
● 由：。
● 兩邊除以零，得出。
● 化簡，得：。
以上謬論一個假設，就是某數除以0是容許的，並且。
若某數學系統遵從域的公理，則在該數學系統內除以零必須為沒有意義。這是因為除法被定義為是乘法的逆向操作，即 值是方程 中 的解（若有的話）。若設，方程式 可寫成 或直接。因此，方程 沒有解（當 時），但是任何數值也可解此方程（當 時）。在各自情況下均沒有獨一無二的數值，所以未能下定義。
整數，是序列中所有的數的統稱，包括負整數、零（0）與正整數。和自然數一樣，整數也是一個可數的無限集合。這個集合在數學上通常表示為粗體Z或，源於德語單詞Zahlen（意為“數”）的首字母。
在代數數論中，這些屬於有理數的一般整數會被稱為有理整數，用以和高斯整數等的概念加以區分。
全體整數關於加法和乘法形成一個環。環論中的整環、無零因子環和唯一分解域可以看作是整數的抽象化模型。
Z是一個加法循環群，因為任何整數都是若干個1或 -1的和。1和 -1是Z僅有的兩個生成元。每個元素個數為無窮個的循環群都與（Z,+）同構。
基本信息
- 中文名
- 有理數
- 外文名
- rational number
- 提出時間
- 約公元前580年至公元前500年間
- 拼音
- yǒu lǐ shù
- 定義
- 數與代數領域中的重要內容之一，是繼續學習實數、代數式、方程、統計等數學內容以及相關學科知識的基礎
- 應用學科
- 數學
- 所屬範圍
- 實數
- 對應概念
- 組成
- 整數，分數