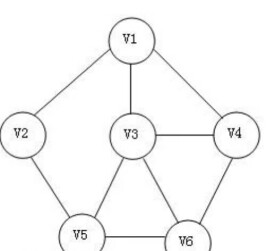
無向圖
每條邊都是無方向的圖
無向圖指是一個二元組
無向圖其中:
1.V是非空集合,稱為頂點集。
2.E是V中元素構成的無序二元組的集合,稱為邊集。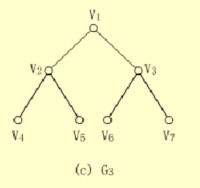

無向圖
直觀來說,若一個圖中每條邊都是無方向的,則稱為無向圖。
(1)無向邊的表示
無向圖中的邊均是頂點的無序對,無序對通常用圓括弧表示。
【例】無序對(vi,vj)和(vj,vi)表示同一條邊。
(2)無向圖的表示
【例】下面(b)圖中的和圖中的G3均是無向圖,它們的頂點集和邊集分別為:
注意:
在以下討論中,不考慮頂點到其自身的邊。即若或是E(G)中的一條邊,則要求。此外,不允許一條邊在圖中重複出現,即只討論簡單的圖。
3.圖G的頂點數n和邊數e的關係
(1)若G是無向圖,則
恰有條邊的無向圖稱無向完全圖(Undirected Complete Graph)
(2)若G是有向圖,則
恰有n(n-1)條邊的有向圖稱為有向完全圖(Directed Complete Graph)。
注意:
完全圖具有最多的邊數。任意一對頂點間均有邊相連。
【例】上面(b)圖的G2就是具有4個頂點的無向完全圖。