操作特性曲線

（1）抽樣特性曲線和抽樣方案是一一對應關係，也就是說有一個抽樣方案就有對應的一條OC曲線；相反，有一條抽樣特性曲線，就有與之對應的一個抽檢方案。

（2） OC曲線是一條通過（0，1）和（1，0）兩點的連續曲線。

（3） OC曲線是一條嚴格單調下降的函數曲線，即對於p1L（p2）。

由於OC曲線與抽樣方案是一一對應的，故改變方案中的參數必導致OC曲線發生變化。但如何變化呢？它們之間的變化有什麼關係呢？下面分三種情況進行討論。

（1）保持n固定不變，令c變化，則如果c增大，則曲線向上變化，方案放寬；如果c減小，則曲線向下變形，方案加嚴。

（2）保持c不變，令n變化，則如果n增大，則曲線向下變形，方案加嚴；反之n減小，則曲線向上變形，方案放寬。

（3） n，c同時發生變化，則如果n增大而c減小時，方案加嚴；若n減小而c增大時，則方案放寬；若n和c 同時增大或減小時，對OC曲線的影響比較複雜，要看n和c的變化幅度各有多大，不能一概而論。如果n和c盡量減少時，則方案加嚴；對於n和c不同量變化的情況，只要適當選取它們各自的變化幅度，就能使方案在（0，pt）和（pt，1）這兩個區間的一個區間上加嚴，而另一個區間上放寬，這一點對我們是很有用的。

我國不少企業在抽樣檢查時仍沿用百分比抽檢法，所謂百分比抽檢法，就是不論產品的批量大小，都規定相同的判定數，而樣本也是按照相同的比例從產品批中抽取。即如果仍用c表示判定數，用k表示抽樣比例係數，則抽樣方案隨交檢批的批量變化而變化，可以表示為（kN|c）。通過OC曲線與抽樣方案變化的關係很容易弄清楚百分比抽檢的不合理性。因為，對一種產品進行質量檢查，不論交檢產品批的批量大小，都應採取寬嚴程度基本相同的方案。但是採用百分比抽檢時，不改變判定數c，只根據批量不同改變樣本容量n，因而對批量不同的產品批採用的方案的寬嚴程度明顯不同，批量大則嚴，批量小則寬，故很不合理。百分比抽檢實際是一種直覺的經驗做法，沒有科學依據，因此應注意糾正這種不合理的做法。

既然改變參數，方案對應的OC曲線就隨之改變，其檢查效果也就不同，那麼什麼樣的方案檢查效果好，其OC曲線應具有什麼形狀呢？下面就來討論這一問題。

（1）理想方案的特性曲線

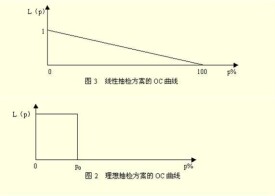
在進行產品質量檢查時，總是首先對產品批不合格品率規定一個值p0來作為判斷標準，即當批不合格品率p≤p0時，產品批為合格，而當p>p0時，產品批為不合格。因此，理想的抽樣方案應當滿足：當p≤p0時，接收概率L（p）=1，當p>p0時，L（p）=0。其抽樣特性曲線為兩段水平線，如下圖所示：

理想方案實際是不存在的，因為，只有進行全數檢查且準確無誤才能達到這種境界，但檢查難以做到沒有錯檢或漏檢的，所以，理想方案只是理論上存在的。

（2）線性抽檢方案的OC曲線

所謂線性方案就是（1|0）方案，因為OC曲線是一條直線而得名的，如下圖所示，

由上圖可見，線性抽檢方案是從產品批中隨機地抽取1個產品進行檢查，若這個產品不合格，則判產品為批不合格品，若這個產品不合格，則判產品批不合格。這個方案的抽樣特性函數為：

因為它和理想方案的差距太大，所以，這種方案的檢查效果是很差的。

理想方案雖然不存在，但這並不妨礙把它作為評價抽檢方案優劣的依據，一個抽檢方案的OC曲線和理想方案的OC曲線接近程度就是評價方案檢查效果的準則。為了衡量這種接近程度，通常是首先規定兩個參數p0和p1（p0