三角形內角和定理

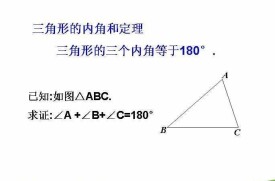
三角形內角和定理：三角形的內角和等於180°。

用數學符號表示為：在△ABC中，∠1+∠2+∠3=180°（見概述圖）。

也可以用全稱命題表示為：∀△ABC, ∠1+∠2+∠3=180°。

在歐式幾何中，∀△ABC, ∠A+∠B+∠C=180°。

三角形：180°=180°·（3-2），

四邊形：360°=180°·（4-2），

五邊形：540°=180°·（5-2），

…，

n邊形：180°·（n-2），…。

任意n邊形內角和公式

任意n邊形的內角和公式為θ=180°·（n-2）。其中，θ是n邊形內角和，n是該多邊形的邊數。從多邊形的一個頂點連其他的頂點可以將此多邊形分成(n-2)個三角形，每個三角形內角和為180°，故，任意n邊形內角和的公式是:θ=（n-2）·180°，∀n=3，4，5，…。

三角形內角和定理

推論1直角三角形的兩個銳角互余。

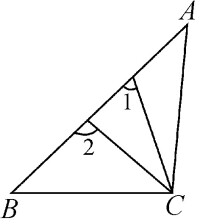
推論2 三角形的一個外角等於和它不相鄰的兩個內角和。

推論3 三角形的一個外角大於任何一個和它不相鄰的內角。

三角形的內角和是外角和的一半。三角形內角和等於三內角之和。.

非歐幾何中的三角形內角和

以上所說的三角形是指平面三角形，處於平直空間中。當三角形處於黎曼幾何空間中時，內角和不一定為180°。例如，在羅巴契夫斯基幾何（羅氏幾何）中，內角和小於180°；而在黎曼幾何時，內角和大於180°。