陣點
陣點
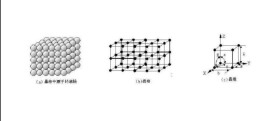
組成晶體的粒子(原子、離子或分子)在三維空間中形成有規律的某種對稱排列,如果我們用點來代表組成晶體的粒子,這些點的總體就稱為空間點陣。點陣中的各個點,稱為陣點。

陣點空間點陣
陣點出發,無論向哪個方向延伸,如果經過一定距離后遇到另一個陣點,那麼再經過相同的距離,必然遇到第三個陣點,如此等等(圖1)。這種距離稱為平移周期。在不同方向上,有不同的平移周期。取一個陣點做頂點,以不同方向上的平移周期a、b、c為棱長,做一個平行六面體。這樣的平行六面體叫做晶胞。如果只要求反映空間點陣的周期性,就可以取體積最小的晶胞,叫做原胞。原胞的重複排列,可以形成整個點陣。原胞的三個棱,可以選作描寫點陣的基本矢量,用a、b、c來表示。選擇任一陣點做原點,點陣中任何一個陣點的矢徑都可以用方程 r=ma+nb+pc 來表示,式中的m、n、p都是整數。由a、b、c的大小和方向決定定整個點陣,所以叫做點陣常數。根據布喇菲(1811~1863)的研究,晶體的構造可分為七大晶系,共有14種不同的點陣。