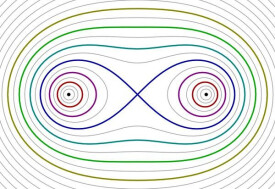
卡西尼卵形線
卡西尼卵形線
發現土星衛星的天文學家喬凡尼卡西尼對把卵形線描繪成軌道有興趣。像笛卡爾卵形線一樣，笛卡爾卵形線 的作法也是基於對橢圓的針線 作法作修改，從而產生更多的卵形曲線。卡西尼卵形線是由下列條件所定義的：曲線上所有點到兩定點（焦點）的距離之積為常數。
卡西尼卵形線是由到兩個定點（叫做焦點）距離之積為常數的所有那些點組成的圖形。
卡西尼卵形線
設兩定點為A，B，AB=2c，動點M滿足MA*MB=a^2(a>0為定值）
當a
當a=c時的分支，成8形自相交叉，稱為雙紐線
當c
當a=c√2時，與前種情況一樣，但曲線中部變平。
當a>c√2時，曲線中部凸起。
卡西尼卵形線圖象由此組成。
取AB為x軸，中點為原點，則
根號[(x+c)^2+y^2]*根號[(x-c)^2+y^2]=a^2
整理得(x^2+y^2)^2-2c^2(x^2-y^2)=a^2-c^4
當a=c時退化為雙紐線方程。
取兩個定點 Q1， Q2為焦點。卡西尼卵形線（Cassini oval）是所有這樣的點P的軌跡： P和焦點的距離的積為常數（這類似橢圓的定義——點 P和焦點的距離的和為常數）。即。
在直角坐標系，若焦點分別在( a，0)和( − a，0)，卵形線的方程可寫成：
(( x− a) + y)(( x+ a) + y) = b( x+ y) − 2 a( x− y) + a= b( x+ y+ a) − 4 ax= b在極坐標系：
r− 2 arcos2θ = b− a卵形線經過反演變換，依然是卵形線。
卵形線的形狀由 b/ a的值決定。若 b/ a> 1，軌跡是一個封閉的圈。若 b/ a< 1，軌跡是兩個封閉的圈。若 b/ a= 1，軌跡為伯努利雙紐線。
基本信息
- 中文名
- 卡西尼卵形線
目錄