開平方
平方的逆運算
定義求一個數a的平方根的運算,叫做開平方(extraction of square root),開平方是平方的逆運算。
求一個數a的平方根的運算,叫做開平方(extraction of square root),其中a叫做被開方數。在實數範圍內a必須大於或等於零,即a為非負數;在複數範圍內,定義i的平方是,即-1的平方根是,記作。
開平方是平方的逆運算,只要我們知道平方的計算方法,開平方就迎刃而解了。
我們令10位數值為A,個位數值為B,即為,根據二數和的平方有:。
舉例說明:例計算方法
1、,
2、,
3、,
4、將這些數,按兩位分節合起來:。得。
將這些計算步驟倒過來,就是開平方。同理,可以得開立方及N次方的方法。
據史料記載,國外直到公元五世紀才有對於開平方法的介紹。
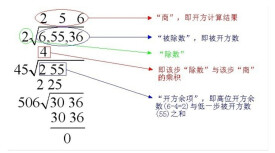
1.將被開方數的整數部分從個位起向左每隔兩位劃為一段,用撇號分開,分成幾段,表示所求平方根是幾位數;
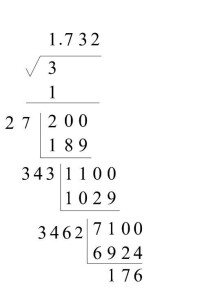
開平方
3.從第一段的數減去最高位上數的平方,在它們的差的右邊寫上第二段數組成第一個餘數(豎式中的256);
4.把求得的最高位數乘以20去試除第一個餘數,所得的最大整數作為試商(除256,所得的最大整數是 4,即試商是4);
5.用所求的平方根的最高位數的20倍加上這個試商再乘以試商.如果所得的積小於或等於餘數,試商就是平方根的第二位數;如果所得的積大於餘數,就把試商減小再試(豎式中,說明試商4就是平方根的第二位數);
6.用同樣的方法,繼續求平方根的其他各位上的數.
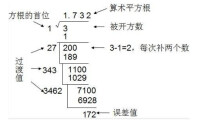
如遇開不盡的情況,可根據所要求的精確度求出它的近似值.
例如求 的近似值(精確到0.01),可列出上面右邊的豎式,並根據這個豎式得到。
筆算開平方運算較繁,在實際中直接應用較少,但用這個方法可求出一個數的平方根的具有任意精確度的近似值.
實例1 開方公式
開平方
5介於2的平方至3的平方;之間。我們取初始值2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9都可以,我們最好取 中間值2.5。
第一步:;輸入值大於輸出值,負反饋;
即,取2位數2.2。
第二步:;輸入值小於輸出值,正反饋;
即,,,。取3位數2.23。
第三步:。
即,,,,取4位數。
每一步多取一位數。這個方法又叫反饋開方,即使你輸入一個錯誤的數值,也沒有關係,輸出值會自動調節,接近準確值。
例如.
200介如10的平方至20的平方之間。初始值可以取11,12,13,14,15,16,17,18,19。我們去15.
。取19也一樣得出14:。
。
.
實例2 精確開方公式
對於一個要開平方的數C,先試估一個儘可能接近方根的數a,使得,且,則
例如,:
因為
所以,一次性得到了7位有效數字的精確度。