拉瓦爾管

一種先收縮后擴張、用以產生超聲速氣流的管道，形狀如圖上部所示，管的橫截面為圓形或矩形。1883年，瑞典工程師C.G.P.de拉瓦爾在他發明的汽輪機中，首先使用這種管道，因而得名。拉瓦爾管廣泛使用於超聲速風洞（見風洞）、噴氣發動機、汽輪機、火箭推進器等需用超聲速氣流的設備中。

拉瓦爾管的原理可用一維定常等熵流動理論來解釋。該理論證明：亞聲速氣流在收縮管中加速，在擴張管中減速；超聲速氣流則相反，在收縮管中減速，在擴張管中加速。拉瓦爾管在正常工作狀態下，亞聲速氣流在收縮段加速，至喉道（即管中橫截面最小處）達到聲速,進入擴張段成為超聲速流，然後繼續加速，直到管出口為止。

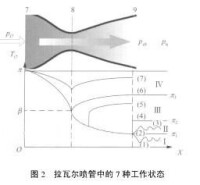
拉瓦爾管的工作狀態由工作壓強比(簡稱壓強比)λ決定。壓強比等於拉瓦爾管入口壓強p0(又稱前室壓強)和出口外壓強（又稱反壓）pe之比。隨著壓強比從小到大的變化，拉瓦爾管內的流動狀態也發生變化。拉瓦爾管的工作狀態在理論上可分為下述六種(沿管軸x方向氣體壓強的分佈見圖下部,pe1、pe2、pe3為由實驗確定的不同數值的反壓):

①當壓強比λ＜p0/pe1時，整個拉瓦爾管內為亞聲速流，壓強分佈曲線為A┡A。

②當壓強比λ=p0/pe1時，喉道截面處流動達到聲速，其餘各截面皆為亞聲速，壓強分佈曲線為A┡B┡B。

③當壓強比為p0/pe1＜λ＜p0/pe2時，喉道下游有一段超聲速區，末端有激波，壓強分佈曲線為A┡B┡CDE。反壓降低，激波后移。

④當壓強比為p0/pe2≤λ＜p0/pe3時，擴張段內全部為超聲速流，管口有激波。管內壓強分佈曲線為A┡B┡CF,壓強pF低於反壓，在出口處激波使氣流壓強增高到等於反壓，整個壓強變化曲線為A┡B┡CFH（若λ=p0/pe2，管內壓強變化曲線為A┡B┡CFG）。這種工作狀態通常稱為過膨脹工作狀態。

⑤λ＝p0/pe3稱為設計壓強比，滿足設計壓強比時，拉瓦爾管擴張段內為超聲速流，管內壓強分佈同狀態

④一樣，出口處氣流壓強恰好等於反壓，無激波也無膨脹波。這種工作狀態稱為設計工作狀態。

⑥當壓強比λ＞p0/pe3時，管內流動和壓強分佈都同設計工作狀態一樣，但出口處氣流壓強高於反壓，經膨脹波降到同反壓相等，這種工作狀態，通常稱為欠膨脹工作狀態。

拉瓦爾管的壁面形狀通常按二維等熵流動或軸對稱流理論計算。