極小曲面
物理學概念
在數學中,極小曲面是指平均曲率為零的曲面。舉例來說,滿足某些約束條件的面積最小的曲面。物理學中,由最小化面積而得到的極小曲面的實例可以是沾了肥皂液后吹出的肥皂泡。肥皂泡的極薄的表面薄膜稱為皂液膜,這是滿足周邊空氣條件和肥皂泡吹制器形狀的表面積最小的表面。
目錄
從變分學觀點看,可以考慮以已知閉曲線Γ為固定邊界的曲面的法向變分。由歐拉-拉格朗日方程(見變分法),對於任何這樣的變分,曲面面積達到臨界值的充要條件是曲面的平均曲率h呏0。因此,通常就用這個幾何條件來定義極小曲面。
在三維歐氏空間中,若一張曲面可用方程來表示,則稱它為圖,或非參數化曲面。由極小條件中極小圖的滿足下述二階非線性橢圓型微分方程:
通常稱它為極小曲面方程。
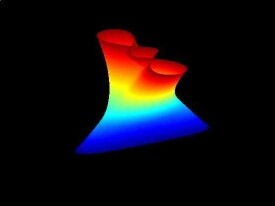
中極小曲面的重要例子有:①極小的可展曲面是平面;②非平面的極小直紋面是正螺面;③懸鏈面是僅有的極小旋轉曲面;④曲率線為平面曲線的極小曲面是恩納佩爾極小曲面;⑤舍克爾極小曲面是極小的螺旋面,它可以看作具有實母曲線的平移極小曲面。一般地,中極小曲面的坐標可表示為等溫參數(使曲面第一基本形式中的,的參數)的調和函數。中不存在緊緻無邊界的極小曲面。
歷史上極小曲面的發展是環繞普拉托問題而展開的,這實質上是一個非線性的橢圓型邊值問題。早在1930~1931年,T.拉多和J.道格拉斯就各自獨立地在廣義解的範圍內解決了這個問題,他們得到如下的存在性定理:給定任一可求長的空間若爾當閉曲線Γ,總存在一張以Γ為邊界的廣義極小曲面。這裡可能有孤立的分支點,在分支點處曲面不是浸入。直到1970年,R.奧斯曼才證明了拉多和道格拉斯的解是處處內部正則的,即不會有分支點。後來丘成桐等又解決了何時浸入化為嵌入的問題。
除了這類存在性問題外,還有不少屬於惟一性方面的問題,其中最著名的是伯恩斯坦定理:中完備的極小圖必是平面。
正如用導數來確定函數的極值一樣,面積泛函的第一變分為零隻是面積最小的必要條件,要進一步確定最小面積的曲面,還必須考慮第二變分。在任何法向變分下,使面積泛函的第二變分恆非負的極小曲面稱為穩定極小曲面。中極小圖是穩定的。因此,從伯恩斯坦定理自然產生這樣的猜想:中完備的穩定極小曲面是平面。這個命題已被D.菲舍爾-科爾布里和 R.舍恩所證明,稍後,M.杜卡莫和彭家貴一起也獨立地予以證明。
對於伯恩斯坦定理在高維空間的推廣,人們很早就提出這樣的問題:設是的完備極小超曲面,那麼函數是否必是線性的?1965年,E.迪喬吉證明是對的;1966年,F.J.阿姆格倫證明也是對的。1967年,J.西蒙斯證明當 時,都是對的。出乎意料的是,E.邦別里、E.迪喬吉和E.朱斯蒂在1968年聯合證得,時,就是不對的。因此,這是一個十分有趣的問題。
參考書目
R. Osserman,A Survey of MiniMal Surfaces,Van Nos-trand-Reinhold, New York, 1969.