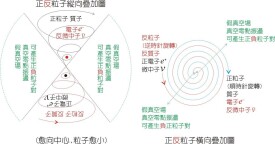
電子波
電子波
電子是一種實物粒子。運動的電子,同樣具有波粒二象性,即可形成電子波。其波長在一定條件下可變得很小,電場和磁場均能使其發生折射和聚焦,從而實現成像,因此,電子波是一種理想的照明光源。
1924年法國物理學家德布羅意(De Broglie)首先提出一個假設:運動的微觀粒子(如電子、中子、離子等)與光的性質之間存在著深刻的類似性,即微觀粒子的運動服從波粒二象性的規律。兩年後通過電子衍射實驗證實了這個假設.得出了著名的德布羅意關係式:
這裡γ是頻率、λ是波長,它們分別是描寫波的物理量;而E是能量、m是質量、v是速度,它們分別是描寫粒子的物理量,通過普朗克常數h,利用德布羅意關係式,把兩者聯繫起來。所以,這組方程體現了微觀粒子的波-粒二象性。也就是說,具有一定動量和能量的電子,也具有一定的波長和頻率。
假設:初速度為零的自由電子e,在電場的作用下,從零電位到達電位為U的電場,將獲得一定的能量,根據能量守恆定律為:由上三式連立,帶入常數換算可得:
當v接近於光速時.電子波長需經相對論校正。不同加速電壓U下的電子波長λ如下表所示。
不同加速電壓下電子波長
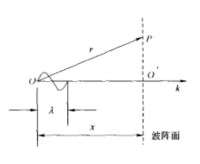
我們知道,入射電子束是單一波長的平面波。平面波的波平面是與其傳播方向垂直的一個平面,如下圖所示,如果入射電子波的波矢量為k,則其波函數可以表示為:
式中,r-波陣面O點到P點的徑矢,如下圖所示;
-入射波的振幅;
-位相角。
電子散射示例
到目前為止,都是假設在晶體內各處入射波的振幅是相同的,忽略了入射波和衍射波之間的相互作用。如果考慮兩束波的相互作用,則必須引入消光距離的概念。人射電子受原子強烈的散射作用,因而在晶體內透射波和衍射波之問的相互作用實際上是不容忽視的。
我們將在簡單的雙光束條件下,即當晶體的(hkl)晶面處於精確的布拉格位向時,入射波只被激發成為透射波和(hkl)晶面的衍射波的情況下,考慮一下兩個波之間的相互作用。
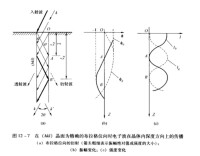
電子波在晶體內深度方向上的傳播
與此同時,我們必須注意到由於入射波與(hkl)晶面交成精確的布拉格角θ。那麼由入射波激發產生的衍射波也與該晶面變成同樣的角度,於是在晶體內逐步增強的衍射波也必將作為新的入射波激發同一晶面的二次衍射,其方向恰好與透射波的傳播方向相同。隨著電子波在晶體內深度方向上的進一步傳播,剛階段的能量轉移過程將以相反的方式在AB階段中被重複,衍射波的強度逐漸下降而透射波的強度相應增大。
這種強烈的動力學相互作用的結果,使和在晶體深度方向上發生周期性的振蕩,如上圖(c)所示。振蕩的深度周期叫做消光距離,記作這裡,“消光”指的是儘管滿足衍射條件,但由於動力學相互作用而在晶體內一定深度處衍射波(或透射波)的強度實際為零。理論推導結果表明
式中,d-晶面間距;
t-原子面上單位面積內所含晶胞數;
θ-布拉格角;
-結構因子;
γ-電子波波長。
軸對稱磁場能使電子束聚焦成像,對電子束起著透鏡的作用。這種磁場由通電流的圓柱形軸對稱線圈產生。透射電子顯微鏡中用磁場來使電子波聚焦成像的裝置是電磁透鏡。為了便於分析電磁透鏡聚焦成像的工作原理,我們以最簡單的電磁透鏡(短線圈磁場的聚焦成像)為例進行分析。根據場的對稱性,將磁場中任意一點A的場強B分解成縱向分量和徑向分量 ,如下圖所示。
通電的短線圈就是一個簡單的電磁透鏡,它能造成一種軸對稱不均勻分佈的磁場。假設以速度為v的電子嚴格地沿著主軸方向射入透鏡內,此時在軸線上磁場強度的徑向分量為零,電子不受磁場力的作用,運動方向不變。若電子是平行於主軸入射,根據右手法則,它將受到所處點磁場強度徑向分量的作用,產生切向力:
使電子獲得切向速度,如下圖(b)所示。電子隨即開始做圓周運動,由於垂直於,產生徑向力:使電子向軸偏轉。當電子穿過線圈到B點位置時, 的方向改變了180°,隨之反向,但是的反向只能使 變小,而不能改變的方向,因此穿過線圈的電子仍然趨向於向主軸靠近。
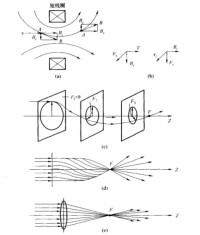
電磁透鏡的聚焦原理示意圖
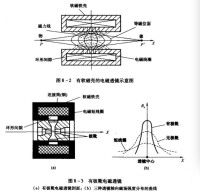
電磁透鏡示意圖