一致最大功效檢驗
一致最大功效檢驗
一致最大功效檢驗(uniformly most powerful test)亦稱一致最強檢驗。簡稱UMP,一種水平a檢驗。
在統計假設檢驗中,一致最大功效檢驗(UMP)是在給定大小α的所有可能測試中具有最大冪β的假設檢驗。例如,根據奈曼 - 皮爾森引理,似然比檢驗是測試簡單(點)假設的一致最大功效檢驗。
一致最大功效檢驗
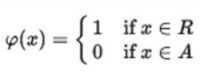
一致最大功效檢驗
這意味著 有效,H就有效,並且如果 有效,H0就有效。注意 是測量空間的不相交的覆蓋。
一個測試函數φ(x)是大小為α的一致最大功效檢驗,對於任何其他測試函數 滿足
一致最大功效檢驗
卡林魯賓定理可以被認為是尼曼 - 皮爾森引理對複合假說的延伸。考慮具有由標量參數θ參數化的概率密度函數的標量測量,並定義似然比
一致最大功效檢驗
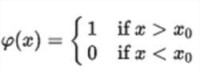
一致最大功效檢驗
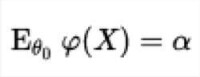
一致最大功效檢驗
請注意,完全相同的測試也是一致最大功效檢驗用於測試H0:θ=θ0,H1:θ>θ0。
儘管由於對標量參數和標量測量的限制,卡林 - 魯賓定理可能看起來很弱,但事實證明存在許多問題。特別地,具有概率密度函數或概率質量函數的一維指數族,
一致最大功效檢驗
一致最大功效檢驗

一致最大功效檢驗
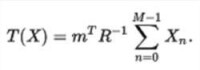
一致最大功效檢驗
一致最大功效檢驗