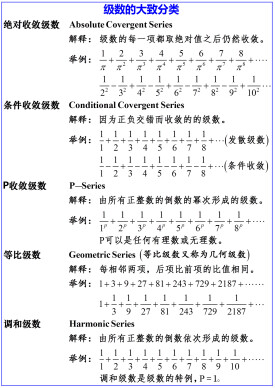
調和級數

早在14世紀，尼克爾·奧里斯姆已經證明調和級數發散，但知道的人不多。17世紀時，皮耶特羅·曼戈里、約翰·伯努利和雅各布·伯努利完成了全部證明工作。

調和序列歷來很受建築師重視；這一點在巴洛克時期尤其明顯。當時建築師在建造教堂和宮殿時，運用調和序列為樓面布置和建築物高度建立比例，並使室內外的建築細節間呈現和諧的聯繫。

因此該級數發散。

通過將調和級數的和與一個瑕積分作比較可證此級數發散。考慮右圖中長方形的排列。每個長方形寬1個單位、高個單位（換句話說，每個長方形的面積都是），所以所有長方形的總面積就是調和級數的和：矩形面積和：而曲線以下、從1到正無窮部分的面積由以下瑕積分給出：曲線下面積：由於這一部分面積真包含於（換言之，小於）長方形總面積，長方形的總面積也必定趨於無窮。更準確地說，這證明了：

這個方法的拓展即積分判別法。

假設調和級數收斂 , 則：

但與矛盾，故假設不真，即調和級數發散。

調和級數發散的速度非常緩慢。舉例來說，調和序列前10項的和還不足100。這是因為調和數列的部分和呈對數增長。特別地，其中是歐拉-馬歇羅尼常數，而約等於，並且隨著 k趨於正無窮而趨於 0。這個結果由歐拉給出。

調和級數的第n個部分和為：也叫作第n個調和數。

第n個調和數與n的自然對數的差值（即）收斂於歐拉-馬歇羅尼常數。

兩個不同的調和數之間的差值永遠不是整數。

除了時以外，沒有任何一個調和數是整數。

很早就有數學家研究，比如中世紀後期的數學家Oresme在1360年就證明了這個級數是發散的。他的方法很簡單：

注意后一個級數每一項對應的分數都小於調和級數中每一項，而且後面級數的括弧中的數值和都為，這樣的有無窮多個，所以後一個級數是趨向無窮大的，進而調和級數也是發散的。

從更廣泛的意義上講，如果是全部不為0的等差數列，則 就稱為調和數列，求和所得即為調和級數，易得，所有調和級數都是發散於無窮的。

隨後很長一段時間，人們無法使用公式去逼近調和級數，直到無窮級數理論逐步成熟。1665年牛頓在他的著名著作《流數法》中推導出第一個冪級數：

Euler(歐拉)在1734年，利用Newton的成果，首先獲得了調和級數有限多項和的值。結果是：

(r為常量)

他的證明是這樣的：

根據Newton的冪級數有：

於是：

代入，就給出：

......

相加，就得到：

後面那一串和都是收斂的，我們可以定義

Euler近似地計算了r的值，約為0.5772156649。這個數字就是後來稱作的歐拉常數。其表達式為：

或者

自然數倒數和逼近公式

c為歐拉常數

解碼函數比原函數偏小，函數在時誤差為-0.0382064988721671，n（2,7）時誤差為0.0257360642441862~0.0106247817461118，時誤差為0.00942087240133116左右，時0.000998481033276377左右n特別大時逐漸時趨於0。誤差就是余函數ε（n）的取值。解碼逼近函數比原函數稍偏小，誤差最大區間是1~7之間。

以下是余函數ε（n）的圖像。

調和級數有以下性質：

我們可以尋找一個函數G(x)，他在定義域內此性質恆成立，且其經過所有的調和級數。

我們暫定其定義域為

則

恆成立

G(x)為連續的凸函數（重要）

則有無數曲線即有無數函數滿足以上要求。我們將其中為凸函數的一個求出，作為調和級數在實數上的合理拓延。

以下求解過程在定義域內完成，不作贅述。

①

②

②-①在除以m得

m趨於無窮小時，g(x)表示G(x)的導數 得

③

因為G(x)為凸函數，所以有以下性質

④

由③④可以推出 為正整數⑤

n趨於正無窮時有

趨於0

所以⑥

由微積分知道 ⑦

此式在非負整數上都成立即調和級數的實數拓延為

註：此式在x趨於無窮時失效，因為那時精度不夠，因為那時被省略的項 所累積的值會逐漸增大， x 趨於正無窮時，該值趨於 ln2。計算方法為將省略項用積分算出。但由於總有省略項的存在，只能得到某種精度的結果。如上式在x 為非無窮時完全成立。

非省略的式子為

此式在用積乘求階乘中十分重要。

中國古代哲學家稱悖論“飾人之心，易人之意，能勝人之口，不能服人之心”。

科學家們通過悖論來提出問題。悖論是科學中基礎理論缺陷的產物，是對科學理論體系的挑戰，是對人類智力的挑戰。研究悖論能使我們了解學科基礎理論的缺陷，而解決悖論的最大意義是能幫我們解決學科基礎理論的缺陷——修改或重建某些基礎理論，從而使科學研究朝著健康的方向發展。這是一種客觀的需要。

約公元前465年，埃利亞的芝諾著述了幾個與無窮概念相關的悖論，導致了科學界的理論危機[1]。2500多年來，許許多多哲學家與數學家努力奮鬥，力圖解決芝諾那些與無窮概念相關的問題，但由於傳統的有窮——無窮理論體系幾千年來沒有什麼實質性的完善[2]，使芝諾悖論不僅不可能得到解決，反而還不時以不同的翻版出現在數學中，固執地向與無窮概念相關的數學內容發出一次次挑戰，並且目標非常清楚——直搗整座數學大廈的基礎。人們到目前為止的所有努力都只能以失敗告終——時間在芝諾悖論面前凝固了！貝特蘭﹒羅素清楚的看到了這一點，他在談及芝諾悖論時寫道：“經過謹慎的解釋，似有可能再現芝諾的所謂‘悖論’，它們從提出之日起直到現在一直被人們所‘駁斥’。”

芝諾悖論不斷以新的形式出現在科學中，形成一個龐大的“芝諾悖論家族”：第二次數學危機是芝諾悖論在300多年前的一種翻版所引起的[3~5]，而我們今天發現的調和級數悖論則是芝諾悖論的又一個很巧妙的翻版。

芝諾悖論

1． 芝諾所著述的與無窮概念相關的悖論

芝諾這些悖論的原作沒有流傳下來，但亞里士多德在其著作中對此作了記錄。我們將與調和級數悖論相關的兩個悖論[1]摘引如下：

a. 運動是不存在的。在跑完某一段距離的全程之前，競賽者首先必須跑完這段距離的一半；在跑完全程的一半之前，又必須跑完一半的半，即全程的四分之一；在跑完全程的四分之一之前，又得跑完全程的八分之一；…… 如此遞推，以至無窮，故運動不可能。

b.阿基里斯追不上烏龜。阿基里斯是古希臘神話中善跑的英雄。在他和烏龜的競賽中，烏龜在前面跑，他在後面追，但他不可能追上烏龜。因為在競賽中，追者首先必須到達被追者的出發點，當阿基里斯到達烏龜在某時所處的位置時，烏龜已向前移動一些；阿基里斯再到達烏龜的那個位置時，烏龜又往前跑了一段；…… 因此，無論阿基里斯到達烏龜曾處的哪個位置，烏龜都會在他前面。所以，無論阿基里斯跑得多快，他永遠追不上烏龜。

芝諾的這些悖論顯然都與人們的生活經驗、共識相悖。但問題是2400多年來人們一直無法真正認識

無窮概念的本質，無法真正認識與之相關的數量形式，必然無法回答芝諾通過悖論要人們所回答的問題。

據說，芝諾的一個學生曾抓來一隻烏龜，讓它在踞自己10步以外向前爬行，然後從後面追上烏龜，演示給芝諾看，想以此來證明阿基里斯完全可以追上烏龜。另一個叫爻布納。希莫尼的學者編了一個既生動有趣、又中肯貼切的對話來評述芝諾悖論的荒謬：當一隻飢餓兇猛的獅子從籠子里被放出來去追趕芝諾時，芝諾不慌不忙地一邊慢跑一邊告訴人家，這隻獅子永遠不可能跑到他身邊。因為獅子首先必須到達他的出發點，當獅子到達他在某時所處的位置時，他已向前移動一些；獅子再到達他的那個位置時，他又往前跑了一段；…… 因此，無論獅子到達他曾處的哪個位置，他都會在獅子前面。所以，無論獅子跑得多快，它永遠追不上他。從另一個角度說，這獅子在接近他時必須跑完全程的一半，在跑完全程的一半前又必須跑完全程的四分之一，在跑完全程的四分之一前又必須跑完程的八分之一，如此類推，以至無窮，獅子連一步都跨不出。但在他剛說完獅子無論如何永遠沒辦法追上他的話音落下后不久，芝諾被這飛跑而至的獅子吞吃掉了。有的人認為象這樣對芝諾悖論的解答是最生動、準確不過了。其實在數學上僅用現在初中生都懂的加和數列就可以輕而易舉地告訴人們阿基里斯何時可追上烏龜。史料也表明芝諾當時未必不懂得這些簡單的常識。但這類解答僅描述了事件的現象和結果，而芝諾要人們解答的是事件的可能性問題，要人們在理論上認識，解釋與無窮概念相關的整個事件的過程。

2500多年前的芝諾以悖論的形式向人們發問：數學中與無窮概念相關的最小的數量形式是什麼、有多大、該如何處理它們？由於這類問題一直無法得到解決，終於又爆發了另一次理論危機，以“微積分中的微增量dx是什麼、有多大、該如何處理它們？”來重複2500多年前芝諾悖論所提出的問題，這就是眾所周知的第二次數學危機。微積分的歷史告訴我們，人們在求導數計算中可以不管dx有多大，想怎樣去稱呼那個dx，打算怎樣去解析與dx相關的那一切數學行為都無所謂，反正按照那些公式如此這般去操作，保證能得出正確的結果。正如芝諾的學生滿足於自己確實能從後面追上烏龜這樣一件事實。但情況並不是這麼簡單！人們公認，第二次數學危機所關心的並不是求導數計算的結果如何，而是象芝諾悖論那樣，關心的是人們該如何從理論上來認識與“無窮”相關的過程、與“無窮”相關的數量形式及其處理方式。由於現代科學中的無窮觀在本質上仍然停留在芝諾時代的那種狀態[2~10]，必然使現代數學中“與無窮概念有關的數量形式及其相關處理方式”的所有理論，不管用什麼語言來表述，在芝諾悖論面前全部原形畢露！無論是在標準分析或非標準分析中，阿基里斯仍然追不上烏龜！所以，公元前465年時的芝諾悖論到如今仍然是芝諾悖論，且由於依然如故的合適的生存條件，使它在2500年中繁殖了許多後代。

2． 調和級數悖論

Oresme於1360年左右在《歐幾里德幾何問題》小冊子中給出了一個關於調和級數發散性的證明。我們可以在現有的，由任何語言所寫的許多數學分析書中看到這個被公認的、很簡單但卻有著不尋常意義的證明（以下簡稱“原證”）。當然是現有的傳統有窮--無窮理論體系及相關的極限論決定了這個證明的產生，使這個證明的整個思路、過程、結果在現有的理論體系框架中被當作共識所普遍接受。但我們的研究恰恰說明這個證明是2500年前芝諾悖論的又一個翻版。

調和級數是個無窮常減級數，Un 0 。級數中出現了人們常說的那種“無窮小”數量形式。在這證明中所暴露的問題仍然是芝諾在2500年前所問的完全相同的問題：無窮小究竟有多大？如何處理它們？

我們將Oresme的證明摘引如下：

（1）

（2）

（3）

（4）

對這個證明有兩種解析：

A. 對級數（1）加上無窮多個括弧而得到一個新的，含有無窮多個大於的數的正數項無窮常增級數（2）；然後，通過sn 的新級數（3）的發散性證得級數（1）發散。

B. 對級數（1）加上許多個括弧而得sn ，在此，k大於任給正數，然後取極限，當n 時，k ，因此sn 而證得級數（1）發散。

原證中的思路與做法是現有數學中傳統的有窮——無窮概念體系和與之相關的極限論很徹底的表現。

對於第一種解釋，承認調和級數中的un 這一事實，原證中那種使用多項式加括弧法則去處理調和級數中的無窮多個un 的數量形式而製造出無窮多個大於的量的思路與做法不妥。這裡我們發現了一個問題：如想對級數（1）加上無窮多個括弧而製造出無窮多個大於的量，就要求級數提供無窮多個被加的量，即需要n 。但是當n 時，按定義，級數中必然出現無數以, ,．．．，．．．的形式所表現的那類數量形式。按照三代數學分析理論中處理X 0的數學內容的作法，我們應該將這些無限趨於0的數量形式從多項式運算式中趕走[3]，導致如此多項式運算的加括弧法則失效，再也沒辦法製造出任何大於1/2的量了。所以，如此加括弧法則僅能處理調和級數中的一部分數項而製造出許多個大於的量，但卻沒有能力處理調和級數中的無窮數項而得到無窮多個大於的量。

退一步說，如果有人想出一些理論，硬說原證中那種對實際情況不做任何分析而無限使用加括弧法對調和級數進行處理的隨心所欲的做法是允許的，我們只要改變原證中的加括弧法則，依法炮製（如使式（2）中的每一項大於1或大於10或大於100……），就可以將調和級數變成任意的正數項無窮常增級數。這樣，一個un 的無窮常減級數就可以用加括弧法象變戲法一樣將其改造成任意的un 的無窮常增級數，反之亦然！難道這樣兩種性質上有很大區別的無窮級數果然真的可以互相轉化？這隻能給原來的“無窮”、“無窮小”、“無窮大”概念再添上一層神秘的色彩。

對於第二種解釋，我們承認可對級數（1）的有窮數項加上有窮多個括弧而得sn ，但如果接下去說“要取極限”，而斷言當n 時，k ，因此sn ，就錯了。與第一種解析中同樣的道理，因為當我們說n 時，實際上就同時承認了這類事實的存在；與求導數過程中的微增量一樣，它們本應該從多項式運算式中消失，而再也沒有“原料”讓那樣的一種多項式加括弧法去製造出任何大於的數了。這決定k根本就不具備趨於 的條件，sn 的推論是完全沒有根據的，是錯誤的！

我們目睹了一個活生生的現代芝諾悖論的翻版：阿基里斯就是這個證明中的多項式加括弧法，而烏龜就是調和級數。儘管善跑的阿基里斯步伐又大又快，但是在理論上烏龜將永遠在他的前面----儘管多項式加括弧法可以很快處理掉調和級數中的許許多多數項，但理論上卻永遠有無數可用多項式加括弧法則去處理的數項。所以那裡的阿基里斯永遠追不上烏龜，而這裡的多項式運算可以得到無窮多個大於的量。

在此，我們清楚地看到，在原證的整個證明中竟然可以完全不必分析級數中的un 是什麼意思，該如何處理它們，為什麼可以那樣處理？比如說，能否象在求導數的運算中那樣，對這些無窮小數項（或叫無限趨於0的量）過一道“ —δ”語言手續，或過一道“取標準數的手續”，而讓它們都從多項式加法運算式中消失，使證明中的加括弧多項式運算沒有條件無窮地進行下去。是數學家把這些問題給忘了嗎？不！問題的關鍵是：在傳統的有窮--無窮理論體系中該在什麼時候、對什麼樣的數學內容取極限，是毫無理論根據的。而更重要的是：從芝諾時代起一直到現在，“無窮”就是個很籠統的數學內容，人們根本無法明確地表現與無窮概念相關的各種數量形式，這必然使人們無法認識調和級數中的un 所表示的數學意義；該如何認識與處理這類與un 有關的無數數項，人們心裡是無數的[6~7]。換句話說，以現有數學中傳統的有窮、無窮理論體系和與之相關的極限論，誰也無法自圓其說：為什麼在數學分析理論的求導數運算中，可以通過對dx取極限或取標準數的做法讓無限趨於零的dx從多項式運算式中消失，而在調和級數中的卻不該從多項式運算式中消失？誰也無法自圓其說：用那樣一種加括弧法則去處理調和級數，究竟能製造出多少個大於1/2的量——有窮多個或無窮多個？當然，在現有的理論體系中，不管是哪種結論都會產生悖論。

結論

2500多年前，芝諾以悖論的形式向人們發問：無窮過程所產生的無窮小究竟是多大、該如何處理它們？而到了三百多年前的微積分時代，貝克萊又以“dx悖論”的形式再版芝諾悖論，重新向人們發問：與無窮概念相關的無限趨於0的量究竟是多大、該如何處理它們？今天，調和級數悖論所提出的問題還是：無窮調和級數中的un 數項究竟是多大、該如何處理它們？2500多年來，這個問題反覆出現，不知要耗費人類多少心血。

2500多年的科學史告訴我們，人們在解決芝諾悖論上的工作思路是錯誤的：沒有深入研究造成悖論的傳統無窮觀及相關數量體系的缺陷，沒有從構造新的無窮觀及相對應的數量體系下手。所以，不管如何努力，只能是徒勞。

掙脫現有的傳統有窮--無窮理論體系缺陷的束縛，構造科學的、新的有窮--無窮理論體系及與之相對應的數量體系，才是徹底解決芝諾悖論、徹底解決所有芝諾悖論翻版，徹底解決第二、第三次數學危機的唯一途徑[6~10]。

當n越來越大時，調和級數的項變得越來越小，然而，慢慢地——非常慢慢地——它的和將增大並超過任何一個有限值。調和級數的這種特性使一代又一代的數學家困惑並為之著迷。下面的數字將有助於我們更好地理解這個級數。這個級數的前1000項相加約為7.485；前100萬項相加約為14.357；前10億項相加約為21；前一萬億項相加約為28，等等。更有學者估計過，為了使調和級數的和等於100，必須把10的43次方項加起來。

調和級數是發散的，這是一個令人困惑的事情，事實上調和級數令人不耐煩地慢慢向無窮大靠近，我們可以很容易的看到這個事實，因為,而調和級數的第一項是1，也就是說調和級數的和要想達到51那麼它需要有2的100次方那個多項才可以。而2的100次方這個項是一個大到我們能夠處理範圍以外的數字，在計算機元科學領域，這屬於一個不可解的數。

p-級數在的時候是收斂的，也就是說對於任意,n的次方的倒數這個級數是收斂的，在我們直觀上看來，好像調和級數下面的n只要大了一小點，或者說調和級數的每一項只要小一小點點，那麼這個級數就是收斂的了，但是事實上並不是這樣這個級數的發散的，但是在的時候,是一個人盡皆知的事實，但是它卻並不收斂，這個令人困惑的問題恰恰說明了一個問題，數軸上數的稠密性。

在分母換成素數的時候又會產生兩個令人困惑不解的事實：

設所有的素數的倒數和為：

在我們直觀的看來，素數比自然數要少的多，但是很不幸這個級數是發散的.

但是在同時所有孿生素數的倒數和:

這個級數是收斂的，現在這個常數就被稱為布隆常數:

另外一個我們取調和級數的一個子數列，例如取,級數仍然是發散的，但是這樣卻產生了另一個困惑，我們如果取n為所有不含有數字8的自然數，所得的級數是收斂的，這個事實可以這樣解釋，在無限的範圍以內，每個自然數幾乎含有所有的10個數字.

:

......

計算機程序（C）：

注意：本程序由於浮點誤差，當時不保證結果準確；但演演算法是正確的，僅供參考。

#include

int main()

{

int k,i=0;

double tot=0;

scanf("%d",&k);

while(tot<=k)

{ i++;

tot+=1.0/i;

}

printf("%d\n",i);

system("pause");

}

或者

#include

int main(void)

{

int i,n;

double sum=0;

printf("please intput n：\n");

scanf("%d",&n);

for(i=1;i<=n;i++)

{

sum+=1.0/i;

printf("%-20.16lf",sum);

}

return 0;

}