動能

運具量，稱。義質量速乘積半。質量，運速越，越；運速，質量越，具越。

械運具，質量速率運，：

概念早..萊布尼茲提；稱，義，義倍。

經典物理中：

動能公式是：，式中，m為物體質量，v為速度。

愛因斯坦在相對論中對上式進行補充，補充后完整的公式是：

，

式中，是靜止質量。

動能的特點：

1）動能是標量；

2）動能具有瞬時性，在某一時刻，物體具有一定的速度，也具有一定的動能，動能是狀態量；

3）動能具有相對性，對不同的參考系，物體速度有不同的瞬時值，也就具有不同的動能，一般以地面為參考系研究物體的運動。

國際單位制中，動能的單位是焦耳。符號：J。

說明：動能是標量，無方向，只有大小，且不能小於零。與功一致，可直接相加減。

動能是相對量，不同的參照系中，v不同，物體的動能也不同。

質點以運動方式所儲存的能量。但在速度接近光速時有重大誤差。狹義相對論則將動能視為質點運動時增加的質量能，修正後的動能公式適用於任何低於光速的質點。

衝量是力對時間的積累效應。力對物體的衝量，使物體的動量發生變化，而且衝量等於物體動量的變化量。

在碰撞過程中，物體相互作用的時間極短，但力卻很大，而且力在這短時間內變化十分劇烈，因此很難對力和物體的加速度做準確的測量；況且這類問題有時也並不需要了解每一時刻的力和速度，而只要了解力在作用時間內的積累作用和它產生的效果。這類問題，雖然原則上可以用牛頓運動定律來研究，但很不方便。為了能簡便地處理這類問題，就需要應用衝量這一概念。

1）動能定理

力在一個過程中對物體所做的功等於在這個過程中動能的變化。

合外力(物體所受的外力的總和,根據方向以及受力大小通過正交法能計算出物體最終的合力方向及大小) 對物體所做的功等於物體動能的變化。

動能定理可以表述為：,即外力對物體做的總功等於物體動能的變化。

在全過程的各個階段受力有變化的情況下，只要把各個力在各個階段所做的功都按照代數和加起來，就可以得到總功。動能定理建立起過程量（功）和狀態量（動能）之間的聯繫。

質點動能定理表達式：

,

其中為末速度，為初速度,其中，表示物體的末動能，表示物體的初動能。△W是動能的變化，又稱動能的增量，也表示合外力對物體做的總功。

動能定理的表達式是標量式，當合外力對物體做正功時，>物體的動能增加；反之則，>，物體的動能減少。

動能定理中的位移，初末動能都應相對於同一參照系。

（1）動能定理研究的對象是單一的物體，或者是可以看成單一物體的物體系。

（2）動能定理的計算式是等式，一般以地面為參考系。

（3）動能定理適用於物體的直線運動，也適用於曲線運動；適用於恆力做功，也適用於變力做功；力可以是分段作用，也可以是同時作用，只要可以求出各個力的正負代數和即可，這就是動能定理的優越性。

2）與牛頓第二定律的區別和聯繫

動能定理是由牛頓第二定律演變而來的，但是這一定理所反映的物理內容卻同牛頓第二定律大不相同，牛頓第二定律反映的是力對物體的作用的瞬時效果，它指出，只要在某一時刻有力作用在物體上，物體便會產生加速度，加速度的大小和方向決定了物體運動狀態將如何變化，而動能定理反映的是力對物體的空間積累效應，它指出，力在某一過程中對物體做了功，物體運動的動能便發生改變。

牛頓第二定律只解決力是恆力、物體沿直線運動的問題，而動能定理既可以解決恆力，直線問題，也可以解決變力、曲線問題，只要不涉及加速度和時間用動能定理比用牛頓第二定律更簡潔明了。

科里奧利是對動能和功給出確切的現代定義的第一個人。他把物體的動能定義為物體質量的二分之一乘以其速度的平方，而作用力對某物體所做的功等於此力乘以其克服阻力而運動的距離。

實驗：探究動能大小與哪些因素有關？

猜想：質量m，速度v

實驗方法：（1）控制變數法，（2）轉換法。

觀察方法：通過觀察木塊被小車推動的距離的遠近來比較小車動能的大小。

實驗過程：

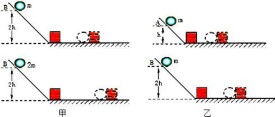
（1）控制小車質量，而通過改變小車在斜面上不同高度，從而改變小車運動到水平面上時的速度。

（2）通過控制小車在斜坡上同一高度下滑從而使不同質量小車到水平面時速度相同。

實驗結論：物體質量相同時，物體運動速度越快，動能越大。物運動速度相同時，質量越大，動能越大。

旋轉動能或角動能是物體旋轉的動能，是物體總動能的一部份。固定參考繫於物體的質心，地球的自轉周期大約是23.93小時。它的角速度是。假設地球形狀是完美的球形，它的質量密度非常的均勻。那麼，它的轉動慣量約為。因此，它擁有旋轉動能2.58E29焦耳。

這樣大的動能，如果能加以利用，肯定會造福人群。借著潮汐能，可以開發出一部分旋轉動能。但這方法也添加了全球性浪潮的摩擦力，微量地減慢了地球的移動速度。依照角動量守恆定律，月亮環繞地球運行的角動量、距離、周期，都會因此增加。

根據動能定理，運動的物體如受到阻礙而減速直到停止以前，物體就會對障礙物作功。所作的功的量等於物體原有動能的量。因此可以說，動能是物體由於運動而具有的作功能力。例如高速飛行的槍彈具有動能，所以打到鋼板上能對鋼扳作功而穿入；捶到鍛件上的鐵鎚具有動能，所以能對鍛件作功而使它變形。

以角速度繞固定軸轉動的剛體，其動能為：

式中I為剛體對轉動軸線的轉動慣量。剛體作平面運動時，其動能為：式中m為剛體的質量，為質心的速度，為剛體對質心軸的轉動慣量，為剛體的角速度。上式可以解釋為：剛體作平面運動時的動能等於剛體以質心速度平動時的動能與剛體相對於質心軸轉動的動能之和。

剛體繞固定點轉動時的動能為：

式中

為剛體對於通過固定點O的三根慣性主軸的轉動慣量，即主慣性矩；為角速度矢的對應慣性主軸上的投影。

剛體作最一般運動的情況下，其動能為：

式中，記號意義和前相似，只是軸就理解為通過質心C的三根慣性主軸。