軟模

軟模概念最先是在研究鐵電相變時明確提出來的（W.科克倫，P.W.安德森，1959,1960）,現在已成為了解結構相變的一個基本概念了。當晶體從順電相轉變為鐵電相時，晶體中發生自發極化，對稱性降低，這時晶體中發生正負離子的相對位移，晶體結構改變（見鐵電性）。按照點陣動力學，晶體中離子對於平衡位置的偏移應以點陣波的形式存在，某種模式的點陣波的頻率反映了對這種模式的偏移的"恢復力"；簡諧近似下，點陣波頻率是與溫度無關的，但實際上總有非諧性，因此點陣波頻率是與溫度有關的。如果在溫度趨於某一數值時，某種（或某幾種）模式的點陣波的頻率趨於零，這便是說點陣對這種模式的偏移的"恢復力"趨於零，點陣對這種偏移成為不穩定了（形象地說，點陣對這種偏移變"軟"了），結果，這種模式的偏移會產生不等於零的靜態值，晶體結構便改變了。如果原來的晶體是順電相，變"軟"的點陣波是極性的──產生電偶極矩，假使其波矢為零，晶體便產生整體的極化，順電相變為鐵電相；假使波矢在布里淵區邊界上（波矢等於ｘ某一倒易點陣矢量），則相鄰元胞的極化相反，便變成反鐵電相（見鐵電性）。這種圖像把從順電相（高對稱相）變到鐵電相(低對稱相)的相變，與高對稱相中某種（或某幾種）模式的點陣波頻率在溫度下降並接近相變溫度時趨於零聯繫起來。類似的，可把從鐵電相(低對稱相)到順電相(高對稱相)的相變，與低對稱相中某種（或某幾種）模式的點陣波頻率在溫度上升趨於相變點時趨於零聯繫起來。人們把這些相變時變"軟"的模式稱"軟模"，前者稱對稱破缺模，後者稱對稱恢復模。一系列的實驗測量（如中子非彈性散射、紅外光譜、散射光譜、磁共振等）證實了這個圖像。圖是碘硫化銻(SBSI)晶體的軟模頻率隨溫度的變化。它的鐵電相變溫度是295K，順電相晶體結構是有反演中心的四方晶系（空間群D），鐵電相變時硫和銻離子沿二次軸偏移，晶體結構變成無對稱中心的四方晶系 (空間群C惌 )；軟模是波矢為零的光頻波，振動模式正是使硫和銻作上述偏移。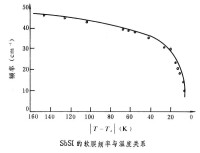上述軟模圖像是與描述結構相變的朗道理論（見固體中的相變）相聯繫的。這時描述相變的序參量是晶體的自發極化強度，它對應於上述圖像中軟模點陣波振幅的靜態值。把系統的自由能對序參量作冪級數展開，它的二次項的係數相應於軟模頻率的二次方。朗道理論把靠近相變溫度時上述二次項係數近似為,A是近似為常數的量。這正相應於軟模頻率在相變溫度時趨於零。朗道相變理論在描述結構相變上是相當成功的。就熱力學性質說，軟模的圖像是與朗道理論相當的。

鐵電相變有幾種不同的類型。上述圖像是位移型相變(見固體中的相變)。還有有序－無序相變和楊-特勒型相變（見楊－特勒效應）。描述這二種相變的序參量不能是選作某種模式的點陣波振幅的靜態值。與之相應，有相應於有序-無序相變的贗自旋模的軟模，相應於楊-特勒相變的電子-點陣模的軟模。其實，軟模概念並不總是只和點陣振動相聯繫的，也並不總是只和鐵電相變相聯繫的。從本質上說相變總伴隨著系統某種對稱性的破缺或恢復，對稱性的破缺或恢復總是與系統的某些運動模式相聯繫的，這些運動模式的激發頻率，在趨於相變溫度時應有軟化現象。因此軟模是一個廣泛的概念。用軟模圖像分析相變時，要注意軟模與其他運動模式的耦合，這使問題複雜了，而且帶來一些新的效應。另外，實際上軟模常常是嚴重阻尼的；上述軟模圖像對應於略去阻尼的情況，軟化表現為振動的力常數（正比於頻率的二次方）在趨於相變溫度時趨於零，近似表達為正比於。另一種極端情況是阻尼很大, 軟化表現為阻尼常數在趨於相變溫度時趨於零, 近似為正比於。這兩種情況是有區別的，前者稱共振型軟模，後者稱弛豫型軟模。實際情況當然是在這兩者之間。

軟模圖像在描述結構相變時取得相當的成功，它使得可用不多的幾個參量來概括結構相變中很豐富的物理現象。但是一個更"徹底"的微觀的軟模理論還是沒有的，目前關於這些參量的微觀機理的認識還是很缺乏的。和關於相變的朗道理論的適用範圍相當，軟模的概念用於很靠近相變點的臨界範圍內是有局限性的。強烈的漲落和關聯以及系統的非簡諧性的表現，使得在這個範圍中軟模的概念和圖像要有所發展和修正。實驗上發現的結構相變的臨界指數與朗道理論預言的不符，中心模現象的存在，以及短程有序的"團"的存在，都說明了這點。

參考書目

M. E. Lines and A. M. Glass,Principles and Applications of Ferroelectrics and Related Materials, Clarendon Press, Oxford, 1977.