相量
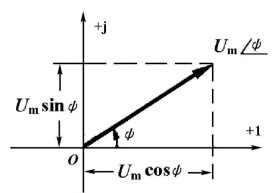
表示正弦量大小和相位的矢量
電路理論中,包括電氣工程和電子信息工程等給出的相量的定義是恆定頻率下的量,是複數,對應複數空間。
分析正弦穩態的有效方法是相量法,相量法的基礎是用一個稱為相量的向量或複數來表示正弦電壓和電流。相量由正弦電壓的振幅Um和初相ψ構成,複數的模表示電壓的振幅,其輻角表示電壓的初相。
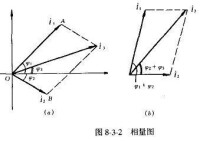
相量圖
相量僅適用於頻率相同的正弦電路。由於頻率一定,在描述電路物理量時就可以只需考慮振幅與相位,振幅與相位用一個複數表示,其中複數的模表示有效值,輻角表示初相位。這個複數在電子電工學中稱為相量.
兩同頻率正弦量疊加,表述為:Asin(ωt+α)+Bsin(ωt+β)=(Acosα+Bcosβ)sinωt+(Asinα+Bsinβ)cosωt.易知,疊加后頻率沒變,相位變化,而且服從相量(複數)運演演算法則。故相量相加可以描述同頻率正弦量的疊加.
相量的的乘除可以表示相位的變化,例如:電感Ι電壓超前電流90度,用相量法表示為U=jχI,其中j為單位複數,χ為感抗.
相量形式的KCL定律表示對於具有相同頻率的正弦電流電路中的任一結點,流出(或流入)該結點的全部支路電流相量的代數和等於零。
相量形式的KVL定律表示對於具有相同頻率的正弦電流電路中的任一迴路,沿該迴路全部支路電壓相量的代數和等於零。
特別注意的是任一結點全部支路電流最大值(或有效值)和沿任一迴路全部支路電壓振幅(或有效值)的代數和並不一定等於零。
一個隨時間按變化的電壓和電流,可以用一個稱為相量的複數來表示。已知正弦電壓電流的瞬時值表達式,可以得到相應的電壓電流相量。反過來,已知電壓電流相量,也能夠寫出正弦電壓電流的瞬時值表達式。
獨立源相量形式
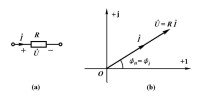
電阻元件相量形式
電阻元件相量形式推導
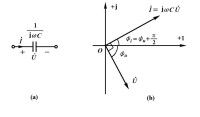
電容元件相量形式
電感元件相量形式推導
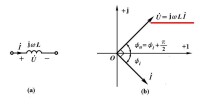
電感元件相量形式
電容元件相量形式推導