倒數
數學學科術語
倒數（reciprocal / multiplicative inverse）是一個數學學科術語，拼音是dào shù。是指數學上設一個數x與其相乘的積為1的數，記為1/x，過程為“乘法逆”，除了0以外的數都存在倒數，分子和分母相倒並且兩個乘積是1的數互為倒數，0沒有倒數。
1.求一個分數的倒數，例如，我們只須把這個分數的分子和分母交換位置，即得的倒數為；
2.求一個整數的倒數，只須把這個整數看成是分母為1的分數，然後再按求分數倒數的方法即可得到。如12，即，再把 這個分數的分子和分母交換位置，把分子做分母，分母做分子，則有，即12倒數是；
3.說明：倒數是本身的數是1和-1，正數的倒數是正數，負數的倒數是負數，0沒有倒數；
4.把0.25化成分數，即，再把這個分數的分子和分母交換位置，把原來的分子做分母，原來的分母做分子。則是，再把化成整數，即4.所以0.25是4的倒數。也可以說4是0.25的倒數。也可以用1去除以這個數，例如0.25，等於4，所以0.25的倒數4；
5.求 倒數的 約分問題。在求倒數過程中，可約分的要約分，如，約分以後成，最後將其分子分母調換位置，得到，即為的倒數；
因此 乘積是1的兩個數 互為倒數。
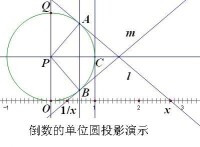
圖1.倒數的單位元投影演示
而在數論中，還有數論倒數的概念，如果兩個數a和b，它們的乘積關於模m餘1，那麼我們稱它們互為關於模m的數論倒數。比如，所以3是2關於5的數論倒數。數論倒數在中國剩餘定理中非常重要。而輾轉相除法提供了計算數論倒數的方法。
近世代數中有群，域，環等概念，其中定義了抽象的乘法運算和單位元。同樣的，關於其乘法如果有乘法逆，同樣可以看成是倒數。
倒數的特點：一個正實數（1除外）加上它的倒數 一定大於2。
理由：, 為倒數當時 一定大於1，可寫為因為，又因為，所以，所以，所以，所以一個正實數加上它的倒數一定大於2。
當時也一樣。
同理可證，一個負實數（-1除外）加上它的倒數一定小於-2。
求證：a，b均為非1正實數，且a不等於b，和互為倒數， 。
證明：因為， ，所以，又因為a，b均為非1正實數，且a不等於b，所以， ，所以，所以，即。
在四則混合運算中，有時會用到倒數來解題，正規解起來很麻煩。
例如：計算
第一種方法：
解：原式的倒數=
=
=
=
=
所以，原式=
第二種方法：
解：=
它的倒數為
=因為此處0不可以作為除數，故用乘法代替。
=
=
所以，原式=
乘積為-1的兩個實數互為負倒數，實數x的負倒數記為或。一個實數的倒數和其負倒數是相反數，0沒有倒數或負倒數。
基本信息
- 中文名
- 倒數
- 外文名
- reciprocal/multiplicative inverse
- 別名
- 乘法逆元
- 表示
- 1/x
- 舉例
- 4/3的倒數是3/4
- 學科
- 數學