圓的一般方程
一個關於x和y的二次方程
圓的一般方程,是數學領域的知識。圓的一般方程為 x+y+Dx+Ey+F=0 (D+E-4F>0),或可以表示為(X+D/2)+(Y+E/2)=(D+E-4F)/4
圓是最常見的、最簡單的一種二次曲線。
在平面上到一定點(中心)有同一距離(半徑)之點的軌跡叫做圓周,簡稱圓。
圓半徑的長度定出圓周的大小,圓心的位置確定圓在平面上的位置。如果已知:(1)圓半徑長R;(2)中心A的坐標(a,b),則圓的大小及其在平面上關於坐標軸的位置就已確定(如右圖)。根據圖形的幾何尺寸與坐標的聯繫可以得出圓的標準方程。結論如下:
當圓的中心A與原點重合時,即原點為中心時,即a=b=0,圓的方程為:
圓的標準方程是一個關於x和y的二次方程,將它展開並按x、y的降冪排列,得: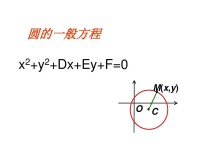

圓的一般方程
設 ;則方程變成:
圓的標準方程是一個關於x和y的二次方程,將它展開並按x、y的降冪排列,得:
任意一個圓的方程都可寫成上述形式。把它和下述的一般形式的二元二次方程比較,可以看出它有這樣的特點:(1)x 項和y 項的係數相等且不為0(在這裡為1);(2)沒有xy的乘積項。
由圓的標準方程的左邊展開,整理得
在這個方程中,如果令
則這個方程可以表示成
可以證明,形如一般表示一個圓。
為此,將一般方程配方,得:
為此與標準方程比較,可斷定:
(1)當>0時,一般方程表示一個以為圓心,為半徑的圓。
(2)當=0時,一般方程僅表示一個點,叫做點圓(半徑為零的圓)。
(3)當<0肘,沒有一個點的坐標滿足圓的一般方程,即一般方程不表示任何圖形,叫做虛圓。
圓的標準方程的優點在於它明確地指出了圓心和半徑,而一般方程突出了方程式上的特點,便於區分曲線的形狀。
求方程的軌跡。
解:這個方程的x 和y 項的係數都是1,並且沒有xy項,它與圓的方程有相同的形式.我們把它配方,
得:
即:
由此可知,原方程的軌跡是一個以點(1,-2)為圓心,4為半徑的圓。
