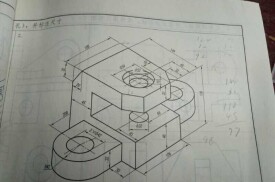
軸測圖
單面投影圖
軸徠測圖是一種單面投影圖,在一個投影面上能同時反映出物體三個坐標面的形狀,並接近於人們的視覺習慣,形象、逼真,富有立體感。但軸測圖一般不能反映出物體各表面的實形,因而度量性差,同時作圖較複雜。因此,在工程上常把軸測圖作為輔助圖樣,來說明機器的結構、安裝、使用等情況,在設計中,用軸測圖幫助構思、想象物體的形狀,以彌補正投影圖的不足。
用平行投影法將物體連同確定該物體的直角坐標系一起沿不平行於任一坐標平面的方向投射到一個投影面上,所得到的圖形,稱作軸測圖。
軸測投影屬於單面平行投影,它能同時反映立體的正面、側面和水平面的形狀,因而立體感較強,在工程設計和工業生產中常用作輔助圖樣。
工程上一般採用正投影法繪製物體的投影圖。即多面正投影圖,它能完整,準確地反映物體的形狀和大小,且質量性好,作圖簡單,但立體感不強,只有具備一定讀圖能力的人才看得懂。有時工程上還需採用一種立體感較強的圖來表達物體,即軸測圖。軸側圖是用軸測投影的方法畫出來的富有立體感的圖形,他接近人們的視覺習慣,但不能確切地反映物體真實的形狀和大小,並且作圖較正投影複雜,因而在生產中它作為輔助圖樣,用來幫助人們讀懂正投影視圖。
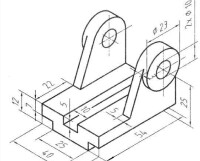
軸測圖
軸測圖根據投射線方向和軸測投影面的位置不同可分為兩大類:
正軸測圖:投射線方向垂直於軸測投影面。
斜軸測圖:投射線方向傾斜於軸測投影面。
根據不同的軸向伸縮係數,每類又可分為兩種:
1.正軸測圖
正等軸測圖(簡稱正等測): p1=q1=r1。
正二軸測圖(簡稱正二測):p1=r1≠q1。
正三軸測圖(簡稱正三測): p1≠q1≠r1。
2.斜軸測圖
斜等軸測圖(簡稱斜等測): p1=q1=r1。
斜二軸測圖(簡稱斜二測): p1=r1≠q1。
斜三軸測圖(簡稱斜三測): p1≠q1≠r1。
由於計算機繪圖給軸測圖的繪製帶來了極大的方便,軸測圖的分類已不像以前那樣重要,但工程上常用的是兩種軸側圖:正等測和斜二測。
(1)相互平行的兩直線,其投影仍保持平行;
(2)空間平行於某坐標軸的線段,其投影長度等於該坐標軸的軸向伸縮係數與線段長度的乘積。
由以上性質,若已知各軸向伸縮係數,在軸測圖中即可畫出平行於軸測軸的各線段的長度,這就是軸測圖中“軸測”兩字的含義。
正等軸測圖:軸間角均為120度;軸向伸縮係數p=q=r =0.82取1
斜二軸測圖:軸間角為90度、135度、135度;軸向伸縮係數p=r=1 q=0.5
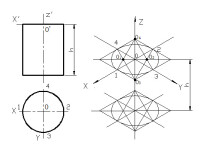
軸測圖是把空間物體和確定其空間位置的直角坐標系按平行投影法沿不平行於任何坐標面的方向投影到單一投影面上所得的圖形。
軸測圖具有平行投影的所有特性:
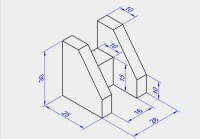
軸測圖
2.定比性:物體上兩平行線段或同一直線上的兩線段長度之比,在軸測圖上保持不變。
3.實形性:物體上平行軸測投影面的直線和平面,在軸測圖上反映 實長和實形。
當投徠射方向 S 垂直於投影面時,形成正軸測圖;當投射方向 S 傾斜於投影面時,形成斜軸測。
1.軸間角和軸向伸縮係數
(1)在正等軸測圖中,三個軸間角相等,都是120°。其中OZ軸規定畫成鉛垂方向。
(2)三個軸向伸縮係數相等,即 p 1 = q 1 = r 1 =0.82。
為了簡化作圖,可以根據GB/T14692-1993採用簡化伸縮係數,即p 1 = q 1 = r 1 =1。從圖6.2.1-1中可以看出,採用簡化伸縮係數畫出的正等軸測圖,三個軸向尺寸都放大了約1.22倍,但這並不影響正等軸測圖的立體感以及物體各部分的比例。
2.平面立體正等軸測圖的畫法
作平面立體正等 軸測圖的最基本的方法是坐標法,對於複雜的物體,可以根據其形狀特點,靈活運用疊加法、切割法等作圖方法。
1.斜二軸測圖的軸間角和軸向伸縮係數
(1)三個軸間角依次為:XOZ=90°、XOY= YOZ =135°。其中OZ軸規定畫成鉛垂方向。
(2)三個軸向伸縮係數分別為:p 1 = r 1 =0.82 、q 1 = 0.5。為了簡化作圖取 p 1 = r 1 =1。
圖片
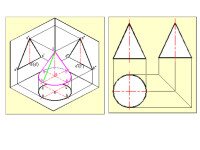
因此,斜二軸測圖主要用於表示僅在一個方向上有圓或圓弧的物體,當物體在兩個或兩個以上方向有圓或圓弧時,通常採用正等測的方法繪製軸測圖。
用菱形法繪製水平圓的正等軸測圖
根據物體的特點,建立合適的坐標軸,然後按坐標法畫出物體上各頂點的軸測投影,再由點連成物體的軸測圖。
正六稜柱正等軸測圖
A. 在視圖上確定坐標原點和坐標軸。
B. 作軸測軸,然後按坐標分別作出頂面各點的軸測投影,依次連接起來,即得頂面的軸測圖I Ⅱ Ⅲ Ⅳ V Ⅵ。
C. 過頂面各點分別作 OZ 的平行線,並在其上向下量取高度 H ,得各棱的軸測投影。
D. 依次連接各棱端點,得底面的軸測圖,擦去多餘的作圖線並加深,即完成了正六稜柱的正等軸測圖。
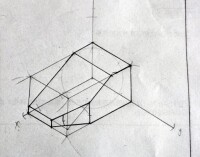
用疊加法畫正等軸測圖
根據圖所示平面立體的三視圖,疊加法畫其正等軸測圖。
將物體看作由 I 、Ⅱ兩部分疊加而成。
A. 畫軸測軸,定原點位置,畫 I 部分的正等測圖。
B. 在 I 部分的正等軸測圖的相應位置上畫出Ⅱ部分的正等軸測圖。
C. 在 I 、Ⅱ部分分別開槽,然後整理、加深即得這個物體的正等軸測圖。
用疊加法繪製軸測圖時,應首先進行形體分析,並注意各形體。
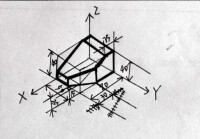
用切割法畫正等軸測圖
1.對所畫物體進行形體分析,搞清原體的形體特徵,選擇適當的軸測圖;
2.在原投影圖上確定坐標軸和原點;
3.繪製軸測圖,畫圖時,先畫軸測軸,作為坐標系的軸測投影,然後再逐步畫出;
4.軸測圖中一般只畫出可見部分,必要時才畫出不可見部分。
畫平面立體軸測圖的基本方法是:沿坐標軸測量,按坐標畫出各頂點的軸測圖,該方法簡稱坐標法;對一些不完整的形體;可先按完整形體畫出,然後再用切割方法畫出不完整部分,此法稱為切割法;對另一些平面立體則用形體分析法,先將其分成若干基本形體,然後還逐一將基本形體組合在一起,此法稱為組合法。
由物體的正投影繪製軸測圖,是根據坐標對應關係作圖,即利用物體上的點,線,面等幾何元素在空間坐標系中的位置,用沿軸向測定的方法,確定其在軸測坐標系中的位置從而得到相應的軸測圖。
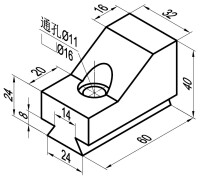
軸測圖