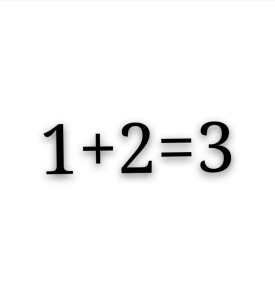加數

加法是基本的四則運算之一，它是指將兩個或者兩個以上的數、量合起來，變成一個數、量的計算。表達加法的符號為加號“+”。進行加法時以加號將各項連接起來。

加法（通常用加號“+”表示）是算術的四個基本操作之一，其餘的是減法，乘法和除法。例如，在下面的圖片中，共有三個蘋果和兩個蘋果的組合，共計五個蘋果。該觀察結果等同於數學表達式“”，即“3加2等於5”。

除了計算水果，也可以計算其他物理對象。使用系統泛化，也可以在更抽象的數量上定義加法，例如整數，有理數，實數和複數以及其他抽象對象，如向量和矩陣。

在算術中，已經設計了涉及分數和負數的加法規則。

加法有幾個重要的屬性。它是可交換的，這意味著順序並不重要，它又是相互關聯的，這意味著當添加兩個以上的數字時，執行加法的順序並不重要。重複加1與計數相同；加0不改變結果。加法還遵循相關操作（如減法和乘法）。

加法是最簡單的數字任務之一。最基本的加法：，可以由五個月的嬰兒，甚至其他動物物種進行計算。在小學教育中，學生被教導在十進位系統中進行數字的疊加計算，從一位的數字開始，逐步解決更難的數字計算。

在以前的教材版本中，規定求兩個數a與b的和時，第一個數a叫被加數，第二個數b叫加數。

而在新教材中，加法算式中，相加的兩個數稱為加數，即不區分加數和被加數。

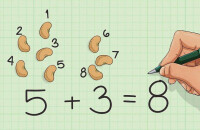
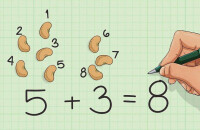
例1：中，哪兩個數是加數？

解：1，2是加數。

可以概括為，中a,b均可稱為加數。

1.若一個加數為0，則和等於另一個加數本身。

2.加一個數，等於減這個數的相反數。

例2：已知，求未知加數x.

解：

∴可以移項得

即

可以概括為：已知加數a，則未知加數

觀察下面等式：

，

人們把具有這種特徵的數叫做卡普列加數，即：對n位自然數N，將N'切分為兩半，右邊n位為一個數，左邊其餘各位為另一個數，如果這兩個數之和恰好等於N那麼稱N和N'為一對卡普列加數，其中N為卡普列加底數，N'為卡普列加平方數。

相傳，關於這類數還有一個故事：數學家卡普列加坐在行駛在從莫斯科到海參崴的西伯利亞的鐵路上，連續的暴雨使得前方發生坍塌，長長的列車被迫停車等候排除險情。幾個小時過去了，太陽已經偏西，焦急的等候使得列車上的乘客心情十分焦躁，數學家卡普列加也正好在這趟列車上，悶熱的天氣驅使他走下列車，百無聊賴得去散步，忽然，他看見一塊鐵路里程碑，木製的牌子被暴風雨劈裂，上面的里程數3025恰好從中間分開，作為數學家的卡普列加馬上發現這個數的與眾不同之處，於是一路上細心研究，收穫頗豐。

“加數乘法”，以前稱過它為“加尾數乘法”和“加前數乘法”，它在兩位數的乘算中，起到了速算的作用。那麼，它在三位數的乘算中，是否也能起到速算的作用？經過多次驗證，還是很適用的。三位數的類型，大體上可分為以下三個類型：

第一類，兩個三位數的乘算，有兩位數是同數，一位數是不同數的三位數，可分為以下三種：

1.百位數、十位數是同數，尾數不是同數的三位數。如…等;

2.十位數、尾數是同數，百位數不是同數的三位數。如…等;

3.百位數、尾數是同數，十位數不是同數的三位數。如…等。

第二類，兩個三位數的延續算，有一位數是同數，兩位數是不同數的三位數。可分為以下三種。

1.百位數是同數，十位數、尾數是不同數的三位數。如…等;

2.十位數是同數，百位數、尾數是不同數的三位數。如…等;

3.尾數是同數，百位數、十位數是不同數的三位數。如…等。

第三類，兩個三位數的乘算，三位數均為不同數的三位數。這種類型的佔大多數。

第一種類型的三位數，它具備了用“加數乘法”計算的條件，也最適用“加數乘法”計算。所以，稱這種類型的三位數，為“有條件”的三位數。

現將“加數乘法”的形成和計算過程、用“交叉乘法”的方式，來表示運算順序，提供廣大珠算愛好者做參考。

舉例如下：

例1：

解：1，（389+84）*3*100=141900

2，

3，

所以

例2

1，

2，

3，

所以原式等於491589。