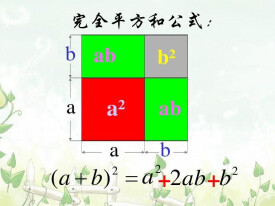
完全平方公式

兩數和的平方，等於它們的平方和加上它們的積的2倍。

兩數差的平方，等於它們的平方和減去它們的積的2倍。

該公式是進行代數運算與變形的重要的知識基礎，是因式分解中常用到的公式。該知識點重點是對完全平方公式的熟記及應用。難點是對公式特徵的理解(如對公式中積的一次項係數的理解等）。

公式特徵（重點）

學會用文字概述公式的含義:

兩數和（或差）的平方，等於它們的平方和，加上（或減去）它們的積的2倍。叫做完全平方公式．為了區別，我們把前者叫做兩數和的完全平方公式，後者叫做兩數差的完全平方公式。

這兩個公式的結構特徵：

● ● 左邊是兩個相同的二項式相乘，右邊是三項式，是左邊二項式中兩項的平方和，加上或減去這兩項乘積的2倍；

● ● 左邊兩項符號相同時，右邊各項全用“+”號連接；左邊兩項符號相反時，右邊平方項用“+”號連接后再“-”兩項乘積的2倍（註：這裡說項時未包括其符號在內）.

● ● 公式中的字母可以表示具體的數（正數或負數），也可以表示單項式或多項式等數學式．

首平方，尾平方，首尾相乘放中間。

或首平方，尾平方，兩數二倍在中央。

也可以是：首平方，尾平方，積的二倍放中央。

同號加、異號減，負號添在異號前。（可以背下來）

即

（注意：後面一定是加號）

（一）、變符號：

例1：運用完全平方公式計算：

（1）

（2）

分析：本例改變了公式中a、b的符號，以第二小題為例，處理該問題最簡單的方法是將這個式子中的(-a)看成原來公式中的a，將(-b)看成原來公式中的b，即可直接套用公式計算。

解答：

(1)原式=

(2)原式=

（二）、變項數：

例2：計算：

分析：完全平方公式的左邊是兩個相同的二項式相乘，而本例中出現了三項，故應考慮將其中兩項結合運用整體思想看成一項，從而化解矛盾。所以在運用公式時，可先變形為，直接套用公式計算。

解答：原式=

（三）、變結構

例3：運用公式計算：

(1)

(2)

(3)

分析；本例中所給的均是二項式乘以二項式，表面看外觀結構不符合公式特徵，但仔細觀察易發現，只要將其中一個因式作適當變形就可以了。

解答：

（1）原式=

（2）原式=

（3）原式=

例4：計算：

（1）

（2）

分析：本例中的999接近1000，100.1接近100，故可化成兩個數的和或差，從而運用完全平方公式計算。

解答：

（1）原式=

（2）原式=

公式的變形：熟悉完全平方公式的變形式，是相關整體代換求知值的關鍵。

例5：已知實數a、b滿足。

求下列各式的值：

（1）

（2）

分析：此例是典型的整式求值問題，若按常規思維把a、b的值分別求出來，非常困難；仔細探究易把這些條件同完全平方公式結合起來，運用完全平方公式的變形式很容易找到解決問題的途徑。

解答：

（1）原式=

（2）原式=

● ● 左邊是一個二項式的完全平方。

● ● 右邊是二項平方的和，加上（或減去）這兩項乘積的二倍，a和b可是數，單項式，多項式。

● ● 不論是還是，最後一項都是加號，不要因為前面的符號而理所當然的以為下一個符號。

● ● 不要漏下一次項。

● ● 切勿混淆公式。

● ● 運算結果中符號不要錯誤。

● ● 變式應用難，不易於於掌握。

● ● 最重要的是做題小心謹慎。