力迫方法是指一種構造公理系統的模型的方法。由P.J.科恩於1963年為證明連續統假設的否定相協調而提出。
一種構造公理系統的模型的方法。由P.J.科恩於1963年為證明連續統假設的否定
力迫方法
與
ZF 相協調而提出,當時證明了
力迫方法
及
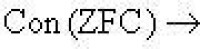
力迫方法
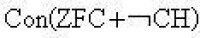
力迫方法
等,其後D.S.斯科特及R.M.索洛韋發展了
布爾值模型處理方法。J.R.休恩菲爾德認識到斯科特及索洛韋的構造可以直接用偏序集而不必嵌入一
完全布爾代數,流行的是休恩菲爾德的既具一般性又與科恩的思想比較接近的處理方法。
給定一個 ZFC的可數可傳模型M。想象一個外來物G,把 G加到 M上擴充成一個可數可傳的M【G】,使得M【G】喺ZFC,M嶅M【G】,G∈M【G】,而且M【G】是具有這三條性質的最小的。在某種意義下,M【G】中的個體是可以由G經過在M中可定義的集論過程得到的。M【G】中的每一個體在M中就能討論,知道G后,就知道M【G】的每一元。一般的情況下G唘M,但是G可以用M中的元素迫近。
為了在M中能討論M【G】,給出一個有很多常量的新語言:令P為一偏序集,P∈M,M喺

力迫方法
ZFC(ctm表示可數可傳模型);定義P-標號,然後令M

力迫方法
{τ∈M|τ是P- 標號}。這些τ∈M可看作形式符號。把原來的語言L={∈}拓展成L
力迫方法
=LU{τ:τ∈M}。這樣的一個P 叫做一個力迫概念,L
力迫方法
叫做T力迫語言,P中的元素叫做力迫條件。兩個條件p,q,在偏序≤下,p≤q稱作p比q強(此處由於歷史因素造成了符號運用的倒置)。一個G吇P,若G是非
空濾子,而且跟每一在M中的稠密子集D吇P有交,則稱為在M上P-脫殊的。給定一個G,不論G∈M與否,可以定義一賦值,使每一τ∈M都有一解釋τG。把所有新常量的G-解釋收集起來成為語言L
力迫方法
的一個結構M【G】

力迫方法
{τG:τ∈M}。對L
力迫方法
一句子ψ,ψ就是M【G】的一個斷言,其真假視 G而定。對p∈P,ψ是L
力迫方法
一句子,定義p
力迫方法
ψ(讀作p力迫ψ)如下:
力迫方法
若M喺

力迫方法
ZFC,P是M中的一偏序集,P0∈P,則總有含有p0的、在M上P-脫殊的G吇P,而且當G是在M上P-脫殊的時候,上面所定義的M【G】喺ZFC,M【G】≥M,G∈M【G】。這樣就從一個模型,擴張成另一個模型。應用不同的
偏序集,可以得到一些附加公理(假設)在 M【G】中成立。相對協調性結果就可如此樣得到。利用這種方法得到的相對協調性結果的數目已經相當可觀了。
力迫方法的很多工作,包括上面那個主定理的證明都用到下面三條引理。
① 可定義性引理 上述
力迫方法
的定義不是能行的。可用
遞歸定義法得到
力迫方法
,使給定p,ψ(τ),p
力迫方法
ψ(τ)對應於L
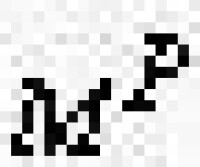
力迫方法
中一T公式,而且p
力迫方法
ψ(τ)匔M喺(p
力迫方法
φ(τ))。
② 真理引理對每一在 M上 P- 脫殊的 G 吇 P,M【G】=φ【τG】匔彐p∈G(p
力迫方法
φ(τ))。
③ 稠密引理對任一L
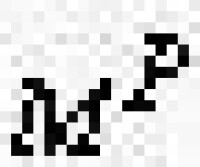
力迫方法
一語句φ(τ),對每一p∈P,都有一比p強的條件q,q或力迫φ(τ),或力迫塡φ(τ)。
以上是力迫的理論。如果想要一個滿足
的模型,就想象一個從ω1到P(ω)的滿射g。G中元素就是這個未知函數g的一些可數迫切。自然令
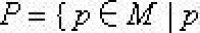
力迫方法

力迫方法
這個P在M中可定義,P ∈M。用

力迫方法
作偏序≤,因此任一在M上P-脫殊的G吇P是一相容函數集, 而且
UG是ω1 到P(ω)的滿射。此處ω1 是在M中看到的第一個不可數基數,P(ω)是M中看到的全體ω的子集。可以由P的性質,證明在M【G】中沒有多出ω的子集來,儘管M【G】確比M大。而且可以證明, 在M【G】中扮演著第一個不可數基數的角色的序數,就是剛才的 ω1,所以M【G】中的函數UG(亦即原來的未知函數 g), 就見證了有一函數,從M【G】認為是第一個不可數的基數,到M【G】認為是ω的全體子集上。即M【G】喺彐g(g是 ω1到P(ω)上的函數)從而M【G】喺
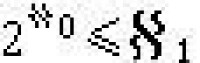
力迫方法
,即M【G】喺CH。這不等於構造了一個CH的模型,而是由一個ZFC的可數可傳模型M,得出一個2FC+CH的可數可傳模型M【G】。
如果取P ={p ∈M|M喺|p|<ω∧p是函數∧dom p吇ω2×ω∧rangep 吇{0,1}},用

力迫方法
作≤,得到的擴張M【G】中至少有堗2個從ω到{0,1}的函數。從而M【G】喺ZFC+塡CH。
為了使在原來的M中作為基數的序數到了M【G】中保持不變,要對力迫概念,也就是偏序集,加上限制。在這個理論的發源期就提出來的有鏈條件和閉性質等,隨著力迫理論方面的突破即迭代力迫的創立,以及J.鮑姆格特納和S.謝拉赫等的正常
力迫法的工作即除了又有許多命題的相對和諧性得到證明之外,提出來的相應的條件又促進了組合集論的發展。


