定態
微觀粒子所處的狀態類型之一
定態是微觀粒子所處狀態中的一種類型的狀態。處於定態的微觀粒子在空間各處出現的幾率不隨時間變化,而且具有確定的能量。
定義:波函數Ψ(x,y,z,t)=Ψ(x,y,z)exp(-i2πEt/h)所描述的狀態
處於定態下的微觀粒子具有如下特徵:能量E具有確定的值;粒子的幾率密度不隨時間改變;所有力學量取各種可能值的幾率分佈及其力學量的平均值都不隨時間而變。在定態中,能量最低的狀態稱為基態(ground state),高於基態的狀態依次稱為第一、第二激發態(excited state)等。當粒子在兩個定態(能量分別為E1和E2)之間躍遷時,將吸收或放出頻率為v的光子,並滿足:El-E2=hv,式中h為普朗克常數。
微觀粒子所處狀態中的一種類型的狀態。處於定態的微觀粒子在空間各處出現的幾率不隨時間變化,而且具有確定的能量。

定態示意圖
定態
當粒子所在的力場不隨時間變化,即U(r,t)=U(r)與時間無關時,上式的解可以寫成

定態
式中E為常量。ψ(r)所滿足的方程為
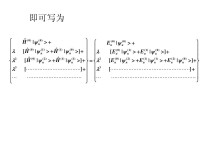
定態
式(1)中的ψ(r,t)所描寫的狀態稱為定態。在定態中,粒子在空間一點r附近出現的幾率與時間無關:|ψ(r,t)|2 =|ψ(r)|2 ,因此,定態的波函數式(1)常常簡單地用ψ(r)來代替。
式(2)常被稱為定態薛定諤方程。在標準條件下解這個方程可以得出E的一組值。對於E的一個值Ei,可以解出相應的定態波函數ψi(r)。量子力學認為,當粒子處於ψi(r)所描寫的狀態時,粒子的能量為Ei,Ei的全部數值的集合, 稱為粒子的能譜。
根據不同情況,能譜可以是分立的,也可以是連續分佈的。
微觀粒子所處狀態中的一種類型的狀態。處於定態的微觀粒子在空間各處出現的幾率不隨時間變化,而且具有確定的能量。
微觀粒子的狀態由波函數ψ(r,t)描寫,ψ(r,t)滿足薛定諤方程定態示意圖(3張)。當粒子所在的力場不隨時間變化,即U(r,t)=U(r)與時間無關時,上式的解可以寫成 , (1)式中E為常量。ψ(r)所滿足的方程為 (2)式(1)中的ψ(r,t)所描寫的狀態稱為定態。在定態中,粒子在空間一點r附近出現的幾率與時間無關:|ψ(r,t)|2=|ψ(r)|2,因此,定態的波函數式(1)常常簡單地用ψ(r)來代替。式(2)常被稱為定態薛定諤方程。在標準條件下解這個方程可以得出E的一組值。對於E的一個值Ei,可以解出相應的定態波函數 ψi(r)。量子力學認為,當粒子處於ψi(r)所描寫的狀態時,粒子的能量為Ei,Ei的全部數值的集合, 稱為粒子的能譜根據不同情況,能譜可以是分立的,也可以是連續分佈的。
概率密度與時間無關。
雖然定態很明顯的含時間。含時間部分是個相位因子。定態的概率密度不含有相位因子這項目。
所以,定態的概率密度與時間無關。一個直接的後果就是期望值也都與時間無關。
所以, 和都與時間無關。一般而言,給予任意一個位置與動量的函數,期望值必然與時間無關。
