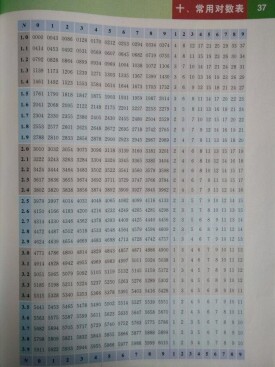
對數表
通過從1開始整數的對數所編排成的表格
對數表是指通過計算得出從1開始各個整數的對數(現在一般用常用對數),所編排成的表格。對數表中不列出首數,它由常用對數的性質確定,真數和對數尾數的精確度取決於對數表的位數,位數越高,精確度越高。
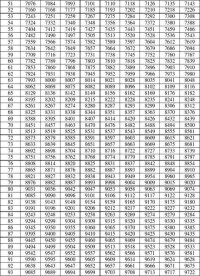 2張
2張對數表
對數表是一種常用的數表。指常用對數表和自然對數表。函數y=lgx的函數值表稱為常用對數表。實際上,表中只列出真數x(1≤x<10)對數尾數的準確值或近似值,因而這樣的表也稱為常用對數尾數表。
根據對數運算的基本公式,可知當因數或除數≠0時,在知道兩大數的對數情況下,可很快計算出兩數的積和商。
如果真數和對數尾數都列出四個有效數字,則稱為四位常用對數表;如果列出五個有效數字,則稱為五位常用對數表。
歷史上,由於常用對數在數值計算中的巨大作用,有許多人投入了編製對數表的工作。
布里格斯(Briggs,H.)於1617年,首先發表了1-100的至小數點八位的常用對數表。
1624年,在布里格斯的《對數算術》中發表1-20000及90000-100000的至小數點14位的常用對數表,其中20000—90000的常用對數表是在弗拉克(Vlacq,A.)的幫助下於1628年編製並發表的。
函數y=Inx的函數值表稱為自然對數表。習慣上的對數表一般值常用對數表。
1、整數部分是一位非零數字。lg2.573:在第1列找25再橫行找“7”為4099,修正值“3”為5。所以lg2.573=0.4104。
2、整數部分不是一位非零數字的。用科學記數示N×10。lg25730=lg(2.573×10)=lg2.573+4=4.4104。
lg0.002573=lg(2.573×10)=lg2.573+(-3)=-2.5896。
3、查反對數時。正小數部分查表,整數部分決定小數點的位置。6.4104:由0.4104查出0.4104=lg2.573。則6.4104=lg2.573+6=lg(2.573×10*6)=lg2573000。負的對數化負整數+正純小數。再同樣查。
對數表
| log | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 表尾差 | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||||
| 10 | 0000 | 0043 | 0086 | 0128 | 0170 | 0212 | 0253 | 0294 | 0334 | 0374 | 4 | 8 | 12 | 17 | 21 | 25 | 29 | 33 | 37 |
| 11 | 0414 | 0453 | 0492 | 0531 | 0569 | 0607 | 0645 | 0682 | 0719 | 0755 | 4 | 8 | 11 | 15 | 19 | 23 | 26 | 30 | 34 |
| 12 | 0792 | 0828 | 0864 | 0899 | 0934 | 0969 | 1004 | 1038 | 1072 | 1106 | 3 | 7 | 10 | 14 | 17 | 21 | 24 | 28 | 31 |
| 13 | 1139 | 1173 | 1206 | 1239 | 1271 | 1303 | 1335 | 1367 | 1399 | 1430 | 3 | 6 | 10 | 13 | 16 | 19 | 22 | 26 | 29 |
| 14 | 1461 | 1492 | 1523 | 1553 | 1584 | 1614 | 1644 | 1673 | 1703 | 1732 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 15 | 1761 | 1790 | 1818 | 1847 | 1875 | 1903 | 1931 | 1959 | 1987 | 2014 | 3 | 6 | 8 | 11 | 14 | 17 | 20 | 22 | 25 |
| 16 | 2041 | 2068 | 2095 | 2122 | 2148 | 2175 | 2201 | 2227 | 2253 | 2279 | 3 | 5 | 8 | 11 | 13 | 16 | 18 | 21 | 24 |
| 17 | 2304 | 2330 | 2355 | 2380 | 2405 | 2430 | 2455 | 2480 | 2504 | 2529 | 2 | 5 | 7 | 10 | 12 | 15 | 17 | 20 | 22 |
| 18 | 2553 | 2577 | 2601 | 2625 | 2648 | 2672 | 2695 | 2718 | 2742 | 2765 | 2 | 5 | 7 | 9 | 12 | 14 | 16 | 19 | 21 |
| 19 | 2788 | 2810 | 2833 | 2856 | 2878 | 2900 | 2923 | 2945 | 2967 | 2989 | 2 | 4 | 7 | 9 | 11 | 13 | 16 | 18 | 20 |
| 20 | 3010 | 3032 | 3054 | 3075 | 3096 | 3118 | 3139 | 3160 | 3181 | 3201 | 2 | 4 | 6 | 8 | 11 | 13 | 15 | 17 | 19 |
| 21 | 3222 | 3243 | 3263 | 3284 | 3304 | 3324 | 3345 | 3365 | 3385 | 3404 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 22 | 3424 | 3444 | 3464 | 3483 | 3502 | 3522 | 3541 | 3560 | 3579 | 3598 | 2 | 4 | 6 | 8 | 10 | 12 | 13 | 15 | 17 |
| 23 | 3617 | 3636 | 3655 | 3674 | 3692 | 3711 | 3729 | 3747 | 3766 | 3784 | 2 | 4 | 6 | 7 | 9 | 11 | 13 | 15 | 17 |
| 24 | 3802 | 3820 | 3838 | 3856 | 3874 | 3892 | 3909 | 3927 | 3945 | 3962 | 2 | 4 | 5 | 7 | 9 | 11 | 12 | 14 | 16 |
| 25 | 3979 | 3997 | 4014 | 4031 | 4048 | 4065 | 4082 | 4099 | 4116 | 4133 | 2 | 3 | 5 | 7 | 9 | 10 | 12 | 14 | 15 |
| 26 | 4150 | 4166 | 4183 | 4200 | 4216 | 4232 | 4249 | 4265 | 4281 | 4298 | 2 | 3 | 5 | 7 | 8 | 10 | 11 | 13 | 15 |
| 27 | 4314 | 4330 | 4346 | 4362 | 4378 | 4393 | 4409 | 4425 | 4440 | 4456 | 2 | 3 | 5 | 6 | 8 | 9 | 11 | 13 | 14 |
| 28 | 4472 | 4487 | 4502 | 4518 | 4533 | 4548 | 4564 | 4579 | 4594 | 4609 | 2 | 3 | 5 | 6 | 8 | 9 | 11 | 12 | 14 |
| 29 | 4624 | 4639 | 4654 | 4669 | 4683 | 4698 | 4713 | 4728 | 4742 | 4757 | 1 | 3 | 4 | 6 | 7 | 9 | 10 | 12 | 13 |
| 30 | 4771 | 4786 | 4800 | 4814 | 4829 | 4843 | 4857 | 4871 | 4886 | 4900 | 1 | 3 | 4 | 6 | 7 | 9 | 10 | 11 | 13 |
| 31 | 4914 | 4928 | 4942 | 4955 | 4969 | 4983 | 4997 | 5011 | 5024 | 5038 | 1 | 3 | 4 | 6 | 7 | 8 | 10 | 11 | 12 |
| 32 | 5051 | 5065 | 5079 | 5092 | 5105 | 5119 | 5132 | 5145 | 5159 | 5172 | 1 | 3 | 4 | 5 | 7 | 8 | 9 | 11 | 12 |
| 33 | 5185 | 5198 | 5211 | 5224 | 5237 | 5250 | 5263 | 5276 | 5289 | 5302 | 1 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 12 |
| 34 | 5315 | 5328 | 5340 | 5353 | 5366 | 5378 | 5391 | 5403 | 5416 | 5428 | 1 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 11 |
| 35 | 5441 | 5453 | 5465 | 5478 | 5490 | 5502 | 5514 | 5527 | 5539 | 5551 | 1 | 2 | 4 | 5 | 6 | 7 | 9 | 10 | 11 |
| 36 | 5563 | 5575 | 5587 | 5599 | 5611 | 5623 | 5635 | 5647 | 5658 | 5670 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 10 | 11 |
| 37 | 5682 | 5694 | 5705 | 5717 | 5729 | 5740 | 5752 | 5763 | 5775 | 5786 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 |
| 38 | 5798 | 5809 | 5821 | 5832 | 5843 | 5855 | 5866 | 5877 | 5888 | 5899 | 1 | 2 | 3 | 5 | 6 | 7 | 8 | 9 | 10 |
| 39 | 5911 | 5922 | 5933 | 5944 | 5955 | 5966 | 5977 | 5988 | 5999 | 6010 | 1 | 2 | 3 | 4 | 5 | 7 | 8 | 9 | 10 |
| 40 | 6021 | 6031 | 6042 | 6053 | 6064 | 6075 | 6085 | 6096 | 6107 | 6117 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 |
| 41 | 6128 | 6138 | 6149 | 6160 | 6170 | 6180 | 6191 | 6201 | 6212 | 6222 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 42 | 6232 | 6243 | 6253 | 6263 | 6274 | 6284 | 6294 | 6304 | 6314 | 6325 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 43 | 6335 | 6345 | 6355 | 6365 | 6375 | 6385 | 6395 | 6405 | 6415 | 6425 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 44 | 6435 | 6444 | 6454 | 6464 | 6474 | 6484 | 6493 | 6503 | 6513 | 6522 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 45 | 6532 | 6542 | 6551 | 6561 | 6571 | 6580 | 6590 | 6599 | 6609 | 6618 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 46 | 6628 | 6637 | 6646 | 6656 | 6665 | 6675 | 6684 | 6693 | 6702 | 6712 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 |
| 47 | 6721 | 6730 | 6739 | 6749 | 6758 | 6767 | 6776 | 6785 | 6794 | 6803 | 1 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 |
| 48 | 6812 | 6821 | 6830 | 6839 | 6848 | 6857 | 6866 | 6875 | 6884 | 6893 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 |
| 49 | 6902 | 6911 | 6920 | 6928 | 6937 | 6946 | 6955 | 6964 | 6972 | 6981 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 |
| 50 | 6990 | 6998 | 7007 | 7016 | 7024 | 7033 | 7042 | 7050 | 7059 | 7067 | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 7 | 8 |
| 51 | 7076 | 7084 | 7093 | 7101 | 7110 | 7118 | 7126 | 7135 | 7143 | 7152 | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 7 | 8 |
| 52 | 7160 | 7168 | 7177 | 7185 | 7193 | 7202 | 7210 | 7218 | 7226 | 7235 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 7 |
| 53 | 7243 | 7251 | 7259 | 7267 | 7275 | 7284 | 7292 | 7300 | 7308 | 7316 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 6 | 7 |
| 54 | 7324 | 7332 | 7340 | 7348 | 7356 | 7364 | 7372 | 7380 | 7388 | 7396 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 6 | 7 |
| 55 | 7404 | 7412 | 7419 | 7427 | 7435 | 7443 | 7451 | 7459 | 7466 | 7474 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 6 | 7 |
| 56 | 7482 | 7490 | 7497 | 7505 | 7513 | 7520 | 7528 | 7536 | 7543 | 7551 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 6 | 7 |
| 57 | 7559 | 7566 | 7574 | 7582 | 7589 | 7597 | 7604 | 7612 | 7619 | 7627 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 6 | 7 |
| 58 | 7634 | 7642 | 7649 | 7657 | 7664 | 7672 | 7679 | 7686 | 7694 | 7701 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 |
| 59 | 7709 | 7716 | 7723 | 7731 | 7738 | 7745 | 7752 | 7760 | 7767 | 7774 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 |
| 60 | 7782 | 7789 | 7796 | 7803 | 7810 | 7818 | 7825 | 7832 | 7839 | 7846 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 6 |
| 61 | 7853 | 7860 | 7868 | 7875 | 7882 | 7889 | 7896 | 7903 | 7910 | 7917 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 6 |
| 62 | 7924 | 7931 | 7938 | 7945 | 7952 | 7959 | 7966 | 7973 | 7980 | 7987 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 6 |
| 63 | 7993 | 8000 | 8007 | 8014 | 8021 | 8028 | 8035 | 8041 | 8048 | 8055 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 64 | 8062 | 8069 | 8075 | 8082 | 8089 | 8096 | 8102 | 8109 | 8116 | 8122 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 65 | 8129 | 8136 | 8142 | 8149 | 8156 | 8162 | 8169 | 8176 | 8182 | 8189 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 66 | 8195 | 8202 | 8209 | 8215 | 8222 | 8228 | 8235 | 8241 | 8248 | 8254 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 67 | 8261 | 8267 | 8274 | 8280 | 8287 | 8293 | 8299 | 8306 | 8312 | 8319 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| 68 | 8325 | 8331 | 8338 | 8344 | 8351 | 8357 | 8363 | 8370 | 8376 | 8382 | 1 | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 6 |
| 69 | 8388 | 8395 | 8401 | 8407 | 8414 | 8420 | 8426 | 8432 | 8439 | 8445 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 6 |
| 70 | 8451 | 8457 | 8463 | 8470 | 8476 | 8482 | 8488 | 8494 | 8500 | 8506 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 6 |
| 71 | 8513 | 8519 | 8525 | 8531 | 8537 | 8543 | 8549 | 8555 | 8561 | 8567 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 5 |
| 72 | 8573 | 8579 | 8585 | 8591 | 8597 | 8603 | 8609 | 8615 | 8621 | 8627 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 5 |
| 73 | 8633 | 8639 | 8645 | 8651 | 8657 | 8663 | 8669 | 8675 | 8681 | 8686 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 5 |
| 74 | 8692 | 8698 | 8704 | 8710 | 8716 | 8722 | 8727 | 8733 | 8739 | 8745 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 5 | 5 |
| 75 | 8751 | 8756 | 8762 | 8768 | 8774 | 8779 | 8785 | 8791 | 8797 | 8802 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 5 | 5 |
| 76 | 8808 | 8814 | 8820 | 8825 | 8831 | 8837 | 8842 | 8848 | 8854 | 8859 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 5 | 5 |
| 77 | 8865 | 8871 | 8876 | 8882 | 8887 | 8893 | 8899 | 8904 | 8910 | 8915 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 78 | 8921 | 8927 | 8932 | 8938 | 8943 | 8949 | 8954 | 8960 | 8965 | 8971 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 79 | 8976 | 8982 | 8987 | 8993 | 8998 | 9004 | 9009 | 9015 | 9020 | 9025 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 80 | 9031 | 9036 | 9042 | 9047 | 9053 | 9058 | 9063 | 9069 | 9074 | 9079 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 81 | 9085 | 9090 | 9096 | 9101 | 9106 | 9112 | 9117 | 9122 | 9128 | 9133 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 82 | 9138 | 9143 | 9149 | 9154 | 9159 | 9165 | 9170 | 9175 | 9180 | 9186 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 83 | 9191 | 9196 | 9201 | 9206 | 9212 | 9217 | 9222 | 9227 | 9232 | 9238 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 84 | 9243 | 9248 | 9253 | 9258 | 9263 | 9269 | 9274 | 9279 | 9284 | 9289 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 85 | 9294 | 9299 | 9304 | 9309 | 9315 | 9320 | 9325 | 9330 | 9335 | 9340 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 86 | 9345 | 9350 | 9355 | 9360 | 9365 | 9370 | 9375 | 9380 | 9385 | 9390 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
| 87 | 9395 | 9400 | 9405 | 9410 | 9415 | 9420 | 9425 | 9430 | 9435 | 9440 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 88 | 9445 | 9450 | 9455 | 9460 | 9465 | 9469 | 9474 | 9479 | 9484 | 9489 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 89 | 9494 | 9499 | 9504 | 9509 | 9513 | 9518 | 9523 | 9528 | 9533 | 9538 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 90 | 9542 | 9547 | 9552 | 9557 | 9562 | 9566 | 9571 | 9576 | 9581 | 9586 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 91 | 9590 | 9595 | 9600 | 9605 | 9609 | 9614 | 9619 | 9624 | 9628 | 9633 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 92 | 9638 | 9643 | 9647 | 9652 | 9657 | 9661 | 9666 | 9671 | 9675 | 9680 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 93 | 9685 | 9689 | 9694 | 9699 | 9703 | 9708 | 9713 | 9717 | 9722 | 9727 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 94 | 9731 | 9736 | 9741 | 9745 | 9750 | 9754 | 9759 | 9763 | 9768 | 9773 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 95 | 9777 | 9782 | 9786 | 9791 | 9795 | 9800 | 9805 | 9809 | 9814 | 9818 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 96 | 9823 | 9827 | 9832 | 9836 | 9841 | 9845 | 9850 | 9854 | 9859 | 9863 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 97 | 9868 | 9872 | 9877 | 9881 | 9886 | 9890 | 9894 | 9899 | 9903 | 9908 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 98 | 9912 | 9917 | 9921 | 9926 | 9930 | 9934 | 9939 | 9943 | 9948 | 9952 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | |
| 99 | 9956 | 9961 | 9965 | 9969 | 9974 | 9978 | 9983 | 9987 | 9991 | 9996 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | |