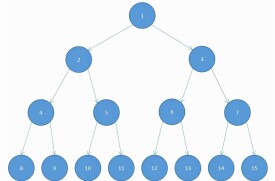
完全二叉樹
效率很高的數據結構
完全二叉樹是效率很高的數據結構,完全二叉樹是由滿二叉樹而引出來的。對於深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。
若設二叉樹的深度為h,除第 h 層外,其它各層 (1~h-1) 的結點數都達到最大個數,第 h 層所有的結點都連續集中在最左邊,這就是完全二叉樹。
完全二叉樹是由滿二叉樹而引出來的。對於深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。
(1)所有的葉結點都出現在第k層或k-l層(層次最大的兩層)
(2)對任一結點,如果其右子樹的最大層次為L,則其左子樹的最大層次為L或L+l。
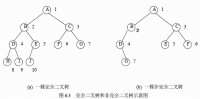
完全二叉樹與非完全二叉樹
如果一棵具有n個結點的深度為k的二叉樹,它的每一個結點都與深度為k的滿二叉樹中編號為1~n的結點一一對應,這棵二叉樹稱為完全二叉樹。
可以根據公式進行推導,假設n是度為0的結點總數(即葉子結點數),n是度為1的結點總數,n是度為2的結點總數,則:
①n= n+n+n(其中n為完全二叉樹的結點總數);又因為一個度為2的結點會有2個子結點,一個度為1的結點會有1個子結點,除根結點外其他結點都有父結點,
②n= 1+n+2*n;由①、②兩式把n消去得:n= 2*n+n-1,由於完全二叉樹中度為1的結點數只有兩種可能0或1,由此得到n=n/2 或 n=(n+1)/2。
簡便來算,就是 n=n/2,其中n為奇數時(n=0)向上取整;n為偶數時(n=1)。可根據完全二叉樹的結點總數計算出葉子結點數。
葉子結點只可能在最大的兩層上出現,對任意結點,若其右分支下的子孫最大層次為L,則其左分支下的子孫的最大層次必為L 或 L+1;
出於簡便起見,完全二叉樹通常採用數組而不是鏈表存儲,其存儲結構如下:
var tree:array[1..n]of longint;{n:integer;n>=1}
對於tree[i],有如下特點:
(1)若i為奇數且i>1,那麼tree的左兄弟為tree[i-1];
(2)若i為偶數且i
(3)若i>1,tree的父親節點為tree[i div 2];
(4)若2*i<=n,那麼tree的左孩子為tree[2*i];若2*i+1<=n,那麼tree的右孩子為tree[2*i+1];
(5)若i>n div 2,那麼tree[i]為葉子結點(對應於(3));
(6)若i<(n-1) div 2.那麼tree[i]必有兩個孩子(對應於(4))。
(7)滿二叉樹一定是完全二叉樹,完全二叉樹不一定是滿二叉樹。
完全二叉樹第i層至多有2^(i-1)個節點,共i層的完全二叉樹最多有2^i-1個節點。
完全二叉樹的特點是:
1)只允許最後一層有空缺結點且空缺在右邊,即葉子結點只能在層次最大的兩層上出現;
2)對任一結點,如果其右子樹的深度為j,則其左子樹的深度必為j或j+1。即度為1的點只有1個或0個
判斷一棵樹是否是完全二叉樹的思路
1>如果樹為空,則直接返回錯
2>如果樹不為空:層序遍歷二叉樹
2.1>如果一個結點左右孩子都不為空,則pop該節點,將其左右孩子入隊列;
2.1>如果遇到一個結點,左孩子為空,右孩子不為空,則該樹一定不是完全二叉樹;
2.2>如果遇到一個結點,左孩子不為空,右孩子為空;或者左右孩子都為空;則該節點之後的隊列中的結點都為葉子節點;該樹才是完全二叉樹,否則就不是完全二叉樹;
#include #include using namespace std; template struct TreeNode { T data; TreeNode TreeNode TreeNode(const T &x) : data(x), left(NULL), right(NULL) {} }; template { //1.樹為空,返回錯誤 if (root == NULL) { return false; } //2.樹不為空 queue q.push(root); while (!q.empty()) { TreeNode //2.1如果該節點兩個孩子都有,則直接pop if (top->left && top->right) { q.pop(); q.push(top->left); q.push(top->right); } //2.2如果該節點左孩子為空,右孩子不為空,則一定不是完全二叉樹 if (top->left == NULL && top->right) { return false; } //2.3如果該節點左孩子不為空,右孩子為空或者該節點為葉子節點,則該節點之後的所有結點都是葉子節點 if ((top->left && top->right == NULL) || (top->left == NULL && top->right == NULL)) { if (NULL != top->left && NULL == top->right) { q.push(top->left); } q.pop(); //則該節點之後的所有結點都是葉子節點 while (!q.empty()) { top = q.front(); if (top->left == NULL && top->right == NULL) { q.pop(); } else { return false; } } return true; } } return true; } //滿二叉樹 void test1() { // 1 // 2 3 // 4 5 6 7 TreeNode TreeNode TreeNode TreeNode TreeNode TreeNode TreeNode node1->left = node2; node1->right = node3; node2->left = node4; node2->right = node5; node3->left = node6; node3->right = node7; cout << IsComplete } //二叉樹為空 void test2() { cout << IsComplete } //3.二叉樹不為空,也不是滿二叉樹,遇到一個結點左孩子為空,右孩子不為空 void test3() { // 1 // 2 3 // 4 5 7 TreeNode TreeNode TreeNode TreeNode TreeNode TreeNode node1->left = node2; node1->right = node3; node2->left = node4; node2->right = node5; node3->right = node7; cout << IsComplete } //4.二叉樹不為空,也不是滿二叉樹,遇到葉子節點,則該葉子節點之後的所有結點都為葉子節點 void test4() { // 1 // 2 3 // 4 5 TreeNode TreeNode TreeNode TreeNode TreeNode node1->left = node2; node1->right = node3; node2->left = node4; node2->right = node5; cout << IsComplete } //4.二叉樹不為空,也不是滿二叉樹,遇到左孩子不為空,右孩子為空的結點,則該節點之後的所有結點都為葉子節點 void test5() { // 1 // 2 3 // 4 5 6 TreeNode TreeNode TreeNode TreeNode TreeNode TreeNode node1->left = node2; node1->right = node3; node2->left = node4; node2->right = node5; node3->left = node6; cout << IsComplete } int main() { test1(); return 0; } |
目錄