西姆松定理
平面幾何定理
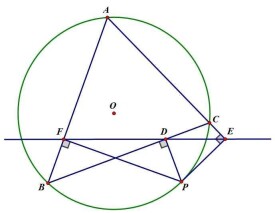
西姆松定理是一個平面幾何定理。其表述為:過三角形外接圓上異於三角形頂點的任意一點作三邊或其延長線的垂線,則三垂足共線。(此線常稱為西姆松線)。西姆松定理的逆定理為:若一點在三角形三邊所在直線上的射影共線,則該點在此三角形的外接圓上。
相關的結果有:
(1)稱三角形的垂心為H。西姆松線和PH的交點為線段PH的中點,且這點在九點圓上。
(2)兩點的西姆松線的交角等於該兩點的圓周角。
(3)若兩個三角形的外接圓相同,這外接圓上的一點P對應兩者的西姆松線的交角,跟P的位置無關。
(4)從一點向三角形的三邊所引垂線的垂足共線的充要條件是該點落在三角形的外接圓上。
證明一:△ABC外接圓上有點P,且PE⊥AC於E,PF⊥BC於F,PD⊥AB於D,分別連FE、FD、BP、CP.
易證P、B、D、F和P、F、C、E分別共圓,(四點共圓)
在PBDF圓內,∠DBP+∠DFP=180度,在ABPC圓內∠ABP+∠ACP =180度,
∴∠DFP=∠ACP ①,在PFCE圓內 ∠PFE=∠PCE
② 而∠ACP+∠PCE=180°
③ ∴∠DFP+∠PFE=180° ④ 即D、F、E共線. 反之,當D、F、E共線時,由④→②→③→①可見A、B、P、C共圓.
證明二:
如圖,若L、M、N三點共線,連結BP,CP,則因PL垂直於

西姆松定理
L分別四點共圓,有
∠NBP = ∠NLP
= ∠MLP= ∠MCP.
故A、B、P、C四點共圓。
若A、P、B、C四點共圓,則
∠NBP= ∠MCP。因PL垂直於BC,PM垂直於AC,PN垂直於AB,
有B、L、P、N和P、M、C、L四點共圓,有
∠NBP = ∠NLP
= ∠MCP
= ∠MLP.
故L、M、N三點共線。
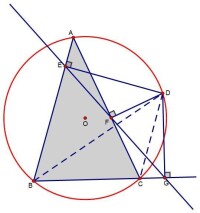
M為線段PH的中點連AH延長線交圓於G。
1.
M為線段PH的中點連AH延長線交圓於G。
證明:連PG交西姆松線與R,BC於Q
如圖連其他相關線段
西姆松定理
PE⊥AC,PF⊥BC==>P.E.F.C共圓==>∠3=∠4
==>∠1=∠4
PF⊥BC
==>PR=RQ
BH⊥AC,AH⊥BC==>∠5=∠6
A.B.G.C共圓==>∠6=∠7
==>∠5=∠7
AG⊥BC==>BC垂直平分GH
==>∠8=∠2=∠4
∠8+∠9=90,∠10+∠4=90==>∠9=∠10
==>HQ//DF
==>PM=MH
2.平分點在九點圓上。
證明:如圖:設O,G,H 分別為三角形ABC的外心,重心和垂心。
則O是,確定九點圓的中點三角形XYZ的垂心,而G還是它的重心。
那麼三角形XYZ的外心 O1,也在同一直線上,並且
HG/GO=GO/GO1=2,所以O1是OH的中點。
三角形ABC和三角形XYZ位似,那麼它們的外接圓也位似。兩個圓的圓心都在OH上,並且兩圓半徑比為1:2
所以G是三角形ABC外接圓和三角形XYZ外接圓(九點圓)的"反"位似中心(相似點在位似中心的兩邊),H 是"正"位似中心(相似點在位似中心的同一邊)。
所以H到三角形ABC的外接圓上的連線中點必在三角形DEF的外接圓上。