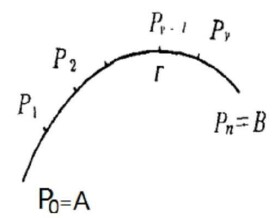
弧長
曲線的特徵之一
曲線的弧長也稱曲線的長度,是曲線的特徵之一。不是所有的曲線都能定義長度,能夠定義長度的曲線稱為可求長曲線。
一般指半徑為R的圓中,n°的圓心角所對弧長為nπR/180°,廣義上指光滑曲線的弧長。
在研究曲線時,我們總引進弧長作為參數,一方面是由於曲線的一般參數 t 不具有任何幾何意義,另一方面,因為弧長是曲線的剛體運動不變數,用弧長作參數,可大大簡化公式,並較容易導出其他不變數。
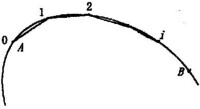
圖1曲線的弧長
曲線有長度的充要條件是其坐標函數為有界變差函數。特別,微分幾何中考慮的類曲線都有長度。曲線Γ在之間的長度可用公式:表示。弧長稱為曲線的 自然參數。
在取自然參數時,曲線的方程:此時,有 (表示對弧長s的 導矢),反之,若,則t可視為曲線從某點量起的弧長參數。
下面我們用微分元素法計算曲線的長度。
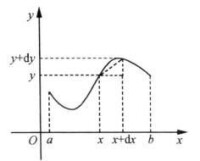
圖2
其中與連續可導,且 ,這樣的稱為 光滑曲線,如圖2.
顯然這時曲線的長度L對於區間可加.且對任意的與小區間相應的弧長
故由微分元素法可知曲線總長為
同樣,對於空間光滑曲線曲線總長為若平面光滑曲線C被表達成了直角坐標形式
則C也有參數表示
故由公式(1)可知這時
例1 證明:圓的周長是。
證明: 由對稱性可知所求周長是第一象限部分長度的4倍,在第一象限中圓的參數方程是
故由公式(1)得圓的周長
半徑為R的圓中,的圓心角所對弧長的計算公式為