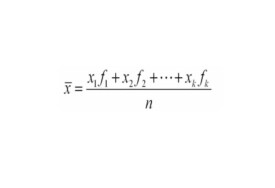加權平均

“統計初步”這部分內容中，平均數是一個非常重要而又有廣泛用途的概念，在日常生活中，我們經常會聽到這樣一些名詞：平均氣溫、平均降雨量、平均產量、人均年收入等；而平均分數、平均年齡、平均身高等名詞更為同學們所熟悉。一般來說，平均數反映了一組數據的一般水平，利用平均數，可以從橫向和縱向兩個方面對事物進行分析比較，從而得出結論。例如，要想比較同一年級的兩個班同學學習成績，如果用每個班的總成績進行比較，會由於班級人數不同，而使比較失去真正意義。但是如果用平均分數去比較，就可以把各班的平均水平呈現出來。從縱向的角度來看，可以對同一個事物在不同的時間內的情況利用平均數反映出來，例如，通過兩個不同時間人均年收入來比較人們生活水平、經濟發展等狀況.

當一組數據中的某些數重複出現幾次時，那麼它們的平均數的表示形式發生了一定的變化。例如，某人射擊十次，其中二次射中10環，三次射中8環，四次射中7環，一次射中9環，那麼他平均射中的環數為:

這裡，7，8，9，10這四個數是射擊者射中的幾個不同環數，但它們出現的頻數不同，分別為4，3，l，2，數據的頻數越大，表明它對整組數據的平均數影響越大，實際上，頻數起著權衡數據的作用，稱之為權數或權重，上面的平均數稱為加權平均數，不難看出，各個數據的權重之和恰為10.

在加權平均數中，除了一組數據中某一個數的頻數稱為權重外，權重還有更廣泛的含義.

在評估某個同學一學期的學生成績時，一般不只看他期末的一次成績，而是將平時測驗、期中考試等成績綜合起來考慮，比如說，一同學兩次單元測驗的成績分別為88，90，期中的考試成績為92，而期末的考試成績為85，如果簡單地計算這四個成績的平均數，即將平時測驗與期中、期末考試成績同等看待，就忽視了期末考試的重要性。鑒於這種考慮，我們往往將這四個成績分配以不同的權重。

由於，即各個權重之和為1，所以求加權平均數的式子中分母為1。

下面的例子是未知權重的情況：

股票A，1000股，價格10；

股票B，2000股，價格15；

算數平均；

加權平均

其實，在每一個數的權數相同的情況下，加權平均值就等於算數平均值。

此外在一些體育比賽項目中，也要用到權重的思想。比如在跳水比賽中，每個運動員除完成規定動作外，還要完成一定數量的自選動作，而自選動作的難度是不同的，兩位選手由於所選動作的難度係數不同，儘管完成各自動作的質量相同，但得分也是不相同的，難度係數大的運動員得分應該高些，難度係數實際上起著權重的作用。