網路圖論
網路圖論
應用圖論研究網路的幾何結構及其基本性質的理論,又稱網路拓撲(network topology)。圖論是離散數學的一個分支,它的研究對象是從實際問題中抽象出來的,用節點(頂點)和支路(邊)構成的線圖(graph),簡稱為圖。
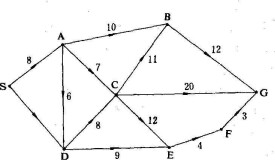
應用圖論研究網路的幾何結構及其基本性質的理論,又稱網路拓撲(network topology)。圖論是離散數學的一個分支,它的研究對象是從實際問題中抽象出來的,用節點(頂點)和支路(邊)構成的線圖(graph),簡稱為圖。例如圖1 (a)中的電網路,其幾何結構可表示成相應的線圖,如圖1 (b)。在線圖中忽略了電路元件的性質,邊的長短與彎曲度都不重要,突出的是節點和支路之間的連接關係。圖2是一公路交通網路的線圖,含有8個節點(城市)和13條支路(公路)。邊上注的字(加權)表示公路長度。用線圖表示的這種連接關係以及由此產生的全部幾何性質又統稱為拓撲性質,故網路圖論又稱為網路拓撲。
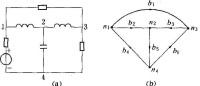
圖1
圖論起源於1736年數學家L.歐拉(L.Euler)求解哥尼斯堡七橋難題。1847年G.R.基爾霍夫(G.R.Kirchhoff)首次用“樹”的概念列出電路方程,並為電網路的拓撲分析奠定基礎。20世紀中葉以後圖論應用日益擴大,涉及網路分析與綜合、計算機輔助設計、電路布圖、信號流圖、電力系統、建築施工以及最短路徑與最大流等方面。隨著計算機應用的普及,圖的演演算法設計成為引人入勝的課題。設計有效演演算法是推廣圖論應用的關鍵。衡量演演算法有效性的主要尺度是運算時間。運算時間可用計算複雜性代替,後者是線圖規模(如圖的節點數)的函數。
從網路的線圖和元件參數可直接求各種常見的網路函數,如單口網路的策動點函數和雙口網路的轉移函數。
1847年G.R.基爾霍夫首先提出一套建立在迴路方程基礎上的網路拓撲公式。此後,J.C.麥克斯韋(J.C.Maxwell)發展了另一套建立在節點方程基礎上的拓撲公式。通常網路函數可通過其節點導納矩陣行列式△=det Yn和它的代數餘子式來表示。上述拓撲公式表明,對於det Yn和其代數餘子式的計算可轉化為直接求網路對應線圖G中全部樹的樹支導納乘積之和與相應的二樹的樹支導納乘積之和,即
△=det Yn=全部的樹支導納乘積之和
△ij=對應的全部二樹的樹支導納乘積之和其中,△ij為△=det Yn中元素(i,j)的餘子式,所謂二樹是指從G的一個樹T中(含n-1個樹支),去掉任一樹支而得到的G的一個子圖。二樹包含G的全部節點,僅有n-2條支路,由兩個分離的子圖組成,每個子圖都不含迴路。以上用枚舉樹以求得網路函數的方法也稱為“k樹法”。並已推廣到含有互感和受控源的有源網路。
信號流圖法是在1953年由S.J. 梅森(S.J.Mason)提出的分析線性系統的拓撲方法。流圖分析包括兩個步驟:先以加權有向圖模擬一個線性系統,再用圖論方法求對應的路徑、迴路數,然後進行運算求得增益。這種方法不僅有效地用來分析反饋控制系統,還可用於熱傳導分析和機械結構分析等。
拓撲分析法的主要優點是計算較為簡便,不像解析法那樣要展開高階行列式,可免除或減少對消冗餘項,提高計算精度,且用線圖模擬系統,形象直觀,物理概念明確;但拓撲法的主要缺點是效率低。隨著網路規模加大,求樹和迴路的計算量將急驟增加,因之一般局限於分析小型網路。
網路圖論還涉及許多非電網路問題。例如在圖2公路交通網路圖中,求S到G的最短路徑。更有實用意義的是求所有節點對間的最短路徑,例如在排定運輸調度計劃,選擇商店、郵局或急救站場址時會用到。這些演演算法可以方便地編製程序上機運算。
早在1962年L.R.福特(L.R.Ford)與D.R.富爾克森(D.R.Fulkson)就發表了第一本研究網路流的專著。在網路流問題中最有代表性的是求最大流問題,即在給定的運輸網路設備條件約束下,可能傳輸的最大流量。在網路流計算中,有個著名的最大流最小切割定理:在運輸網路中,最大流的值等於最小切割的容量。利用這個定理,可方便地求出網路的最大流。1962年L.R.福特與D.R.富爾克森提出的標號演演算法是計算運輸網路中最大流的有效演演算法。網路流演演算法在電力系統網路規劃、安全分析與狀態估計中均得到應用。
網路圖論在理論、演演算法和應用上都存在不少有待解決的問題。特別至今還有許多問題尚未找到有效演演算法,仍值得進一步研究探討。