超越函數
"超出"代數函數範圍的函數
超越函數(Transcendental Functions),指的是變數之間的關係不能用有限次加、減、乘、除、乘方、開方運算表示的函數。
歐拉把約翰·貝努利給出的函數定義稱為解析函數,並進一步把它區分為代數函數(只有自變數間的代數運算)和超越函數(三角函數、對數函數以及變數的無理數冪所表示的函數),還考慮了“隨意函數”(表示任意畫出曲線的函數)。
超越函數是指那些不滿足任何以多項式作係數的多項式方程的函數。說的更技術一些,單變數函數若為代數獨立於其變數的話,即稱此函數為超越函數。
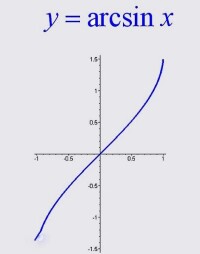
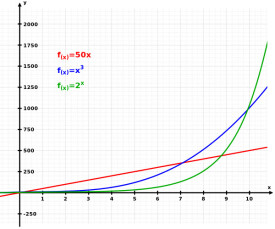
對數和指數函數即為超越函數的例子。超越函數這個名詞通常被拿來描述三角函數。
非超越函數則稱為代數函數。代數函數的例子包括多項式和平方根函數。
一函數的不定積分運算是超越函數的豐富來源,如對數函數便來自倒數函數的不定積分。在微分代數里,人們研究不定積分如何產生與某類“標準”函數代數獨立的函數,例如將三角函數與多項式的合成取不定積分。
在數學領域中,超越函數與代數函數相反,是指那些不滿足任何以多項式方程的函數,即函數不滿足以變數自身的多項式為係數的多項式方程。換句話說,超越函數就是"超出"代數函數範圍的函數,也就是說函數不能表示為有限次的加、減、乘、除和開方的運算。
嚴格的說,關於變數 的解析函數 f() 是超越函數,如果該函數是關於變數是代數獨立的。
對數和指數函數即為超越函數的例子. 超越函數這個名詞通常被拿來描述三角函數,例如正弦,餘弦,正割,餘割,正切,餘切,正矢,半正矢等.
非超越函數則稱為代數函數. 代數函數的例子有多項式和平方根函數.
對代數函數進行不定積分運算能夠產生超越函數. 如對數函數便是在對雙曲角圍成的面積研究中,對倒數函數 = ?x不定積分得到的. 以此方式得到的雙曲函數sinh, cosh, tanh 都是超越函數。
微分代數的某些研究人員研究不定積分如何產生與某類“標準”函數代數獨立的函數,例如將三角函數與多項式的合成取不定積分。