擬合優度
擬合優度
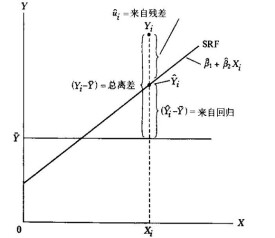
擬合優度(Goodness of Fit)是指回歸直線對觀測值的擬合程度。度量擬合優度的統計量是可決係數(亦稱確定係數)R^2。R^2的取值範圍是[0,1]。R^2的值越接近1,說明回歸直線對觀測值的擬合程度越好;反之,R^2的值越接近0,說明回歸直線對觀測值的擬合程度越差。
R衡量的是回歸方程整體的擬合度,是表達因變數與所有自變數之間的總體關係。R等於回歸平方和在總平方和中所佔的比率,即回歸方程所能解釋的因變數變異性的百分比。實際值與平均值的總誤差中,回歸誤差與剩餘誤差是此消彼長的關係。因而回歸誤差從正面測定線性模型的擬合優度,剩餘誤差則從反面來判定線性模型的擬合優度。
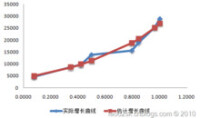
擬合優度曲線圖
金融的應用和解釋:
擬合優度是一個統計術語,是衡量金融模型的預期值和現實所得的實際值的差距。
它是一種統計方法應用於金融等領域,基於所得觀測值的基礎上作出的預測。換句話說,它是衡量如何將實際觀測的數值進行模擬的相關預測。
主要是運用判定係數和回歸標準差,檢驗模型對樣本觀測值的擬合程度。當解釋變數為多元時,要使用調整的擬合優度,以解決變數元素增加對擬合優度的影響。
假定一個總體可分為r類,現從該總體獲得了一個樣本——這是一批分類數據,現在需要我們從這些分類數據中出發,去判斷總體各類出現的概率是否與已知的概率相符。譬如要檢驗一顆骰子是否是均勻的,那麼可以將該骰子拋擲若干次,記錄每一面出現的次數,從這些數據出發去檢驗各面出現的概率是否都是1/6,擬合優度檢驗就是用來檢驗一批分類數據所來自的總體的分佈是否與某種理論分佈相一致。