滲透理論

滲透理論是研究隨機環境中聚簇現象的理論，是Broadbent和Hammersley在1957年研究液體通過多孔媒介問題時提出的。緊接著相變（1960），級數展開（Domb），重整化群等理論的出現和發展進一步幫助了人們理解滲透理論和它作為一種臨界現象的本質。隨後人們在隨機圖理論的研究中發現節點存在節點集群的臨界概率，即網路具有臨界概率p，當不超過p時，網路是由孤立的節點集群組成，但是當超過p時，節點集群將擴展連接到整個網路。滲流理論研究能夠從一端開始而終止於另一端的、可以滲透整個網路的通道出現的概率。

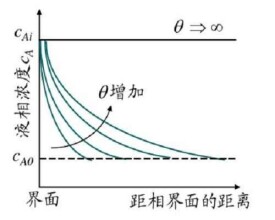
在設備中進行傳質過程而當氣液還未接觸時，整個氣相或液相內的溶質是均勻的。當氣液一開始接觸，溶質才漸漸溶於液相中，隨著氣液接觸時間的增長，積累在液膜內的溶質量也逐漸增多，溶質從相界面向液膜深度方向逐步滲透，直至建立起穩定的濃度梯度。這一段時間稱為過渡時間。按滲透理論預計的傳質速率比雙膜理論的大。本理論建立在雙膜理論的基礎之上，只是強調了形成濃度梯度的過度階段；因討論的是從氣液界面至液相主體的傳質，滲透理論的主要對象為液膜控制的吸收。

現實生活中有許多問題都可以用滲透理論得到合理的解釋。例如，病毒傳播在人群中的傳播問題，設有一個病人，單位時間內他可以以概率p感染他的鄰居，他的受到感染的鄰居又可以以概率p繼續感染鄰居，以此類推。如果傳染概率p很小的話也就是小於滲透出現的臨界概率，那麼疾病的傳播將會停止，如果傳染概率p大於臨界概率pc，疾病將大範圍的傳播。有一塊空地分為兩部分，一部分的表面是沙子，另一部分的表面是粘土。一場大雨過後，為什麼沙子的那一部分沒有存水，另一部分會存水等等一系列的問題都可以用滲透理論進行解釋。

下面我們考慮在二維平面上的情況。我們把這些沙粒比作一個一個的平面上的點，它們之間的邊是可以任意添加的，添加上的邊是允許水通過的。這樣只要是有一個無限遠的通路存在水就可以滲透到地下。

假設通道的規模相對於網格的規模來說太小了的話，這樣這個格子的規模就可以看做是無限的。現在的問題是：存在一個開通邊組成的可以延伸到無限遠的通路的概率是多少？這樣地面上的水就可以滲到地下。

假設參數p屬於[0，1]，並且每條邊開通的概率是p，把開通的這條邊視作一個可以水可以滲透的通道。當p=0，任何一條邊都是閉合的，不存在可以延伸到無限遠的開通路徑。p=1，每一條邊都是開通的，這樣就一定存在延伸到無限遠的開通的路徑。這兩種情況都是沒有研究價值的，下面討論當0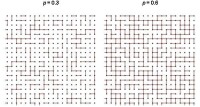

圖1

當p很小的時候，有很少的邊開通，開通的路徑就會非常短。然而，隨著p的增加，開通的邊逐漸增多，最終會出現延伸到無限遠處的路徑。圖1是p=0.3和p=0.6的兩種情況。可以看出，當p從小增大的時候這條通道是會慢慢的出現的。當出現延伸到無限處的通路時，我們就說滲透現象出現了。

當滲透現象剛好出現的概率稱為臨界概率，臨界概率的存在使得滲透理論成為數學上一個有趣和重要的研究課題。存在一個臨界概率，記作pc，當每條邊開通的概率大於Pc時，滲透就會出現，當每條邊開通的概率小於Pc是，滲透就不會出現。所以在臨界概率的兩邊，系統將會出現截然不同的情況。

滲透理論分類

---

邊滲透和點滲透

邊滲透：任意一條邊以概率p聯通，（概率p依賴於邊的性質），當這些聯通的邊聚簇在一起出現無限情況時，成為出現點滲透。

點滲透：任意一點以概率p被佔據，（概率p依賴於點的性質，例如度），當這些佔據的點聚簇在一起出現無限情況時，稱為出現點滲透。每一個邊滲透問題都可被視為點滲透問題，但是反過來不成立。

延伸理論

---

“觀察滲透理論”，是美國科學哲學家漢森提出的著名命題。這個命題指出了我們的任何觀察都不是純粹客觀的，具有不同知識背景的觀察者觀察同一事物，會得出不同的觀察結果。“觀察滲透理論”摧毀了邏輯實證主義所追求的科學合理性。

觀察可分為自然觀察和實驗觀察。自然觀察是指人類對自然現象不作任何人工的變革而進行的一類觀察。實驗觀察是通過對自然現象或事物人為進行積極干預后所進行的觀察。實驗觀察是一種比自然觀察更強有力的認識手段。