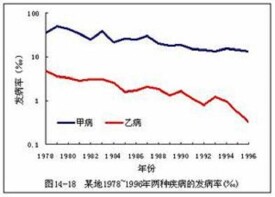
半對數線圖

半對數線圖是一種基本的統計圖形，它與普通線圖（習慣簡稱線圖）一樣均可通過線段的上升或下降來表示一個指標隨另一指標（常為時間）變化而變化的情況。兩者的區別在於普通線圖的橫、縱坐標均為算術尺度，在某兩個不同的時間段上，如果終點相對於起點的“絕對改變數”相同，將在圖形上表現為相同的增幅（或減幅），直觀呈現的是數量變化的態勢；半對數線圖的橫坐標仍為算術尺度（如時間），縱坐標指示的觀察指標（常為研究的指標，如發病率、病死率等）則實施了對數轉換——即對數尺度，在某兩個不同時間段上，如果終點相對於起點的“相對改變數”相同，將在半對數線圖上表現為相同的增幅（或減幅），所以半對數線圖適用於呈現事物發展變化的速度。故兩種圖形從不同的角度反映被觀察指標的變化情況，但二者的意義和適用場合區別甚大，使用時要根據具體情況正確選用。如果研究者一概應用普通線圖來反映動態數據的變化情況，則可能導致無法正確呈現資料所蘊涵的信息。

當研究兩組或多組數據的變化情況時，普通線圖是用來說明研究指標的波動態勢，半對數線圖是用來說明研究指標的變化速度。以兩個觀察指標A與B變化速度的比較為例，在一時間段當指標A發生10→100的變化、指標B發生100→1000變化時，“絕對增長量”分別是90為900，相差較遠；“相對增長量”卻都為10倍於起點水平。顯然，變化速度的比較所注重的恰是“相對增長量”，因此，普通線圖不能對指標A、B的變化速度相等（均為10倍）這一事實給予正確呈現。正確的做法應該是縱坐標採用對數尺度（與線性尺度的橫坐標構成所謂的“半對數線圖”），則前述設定的時間段上的指標A變化量△A=lg100－lg10=1，指標B變化量△B=lg1000－lg100=1，提示指標A與B的發展變化速度相等。

半對數線圖是用來比較兩種或多種事物的相對變化速度。當事物數量間相差較大時，用普通線圖不易正確表達或相互比較，如用半對數線圖，可確切反映出指標數量的相對關係。

因繪製半對數線圖時，縱軸採用對數尺度，橫軸採用算術尺度，故稱為半對數線圖。一般將圖繪製在半對數坐標紙上。

適用於表示事物的發展速度或相對比資料。如表示幾種疾病的發病率或死亡率隨著時間的改變而升降變化速度的比較。

比較所研究指標的變化速度當研究兩組或多組數據的變化情況時，普通線圖用來說明研究指標的波動態勢，半對數線圖用來說明研究指標的變化速度。以兩個觀察指標A和B變化速度的比較為例，在某一時間段當指標A發生10—100的變化、指標B發生100—1000的變化時，“絕對增長量”分別是90和900，相差較遠；“相對增長量”卻都是10倍於起點水平。顯然，變化速度的比較所注重的正是“相對增長量”，因此，普通線圖不能對指標A、B的變化速度相等(均為10倍)這一事實給予正確呈現。正確的做法應該是縱坐標採用對數尺度(與線性尺度的橫坐標構成所謂的“半對數線圖”)，則前述設定的時間段上的指標A變化量A=Ig100-lg10=l，

當根據統計資料選擇統計圖類型時，欲分析其絕對差別應

選普通線圖，當分析其相對差別應選擇半對數線圖。顯然

對於同一資料既要分析其絕對差別的數量變化又要分析其

相對差別的數量變化時，則普通線圖和半對數線圖可以同

時選用。