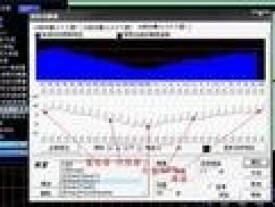
圖形均衡器

下面以 Cool Edit Pro 為例，介紹圖形均衡器（如插圖）。

做音樂最離不開的效果器是什麼？相信大多數朋友都會回答：“是 EQ！”——不錯，正是有了這個所謂“均衡”的效果器，我們的音樂才不會過載，樂器音色才會如此豐富。然而知道 1 加 1 等於 2，更要知道 1 加 1 為什麼等於 2。

“EQ 的原理？聲波是由不同諧波組成的！所謂均衡處理就是改變這些諧波的振幅。”這個說法也對也不對。說它對是因為均衡效果器的初衷是這樣的。說它不對，是因為以當今的數學演演算法，還不能做到由答案推出確定的問題。比如一道題的答案是 10，我的問題可以是 2 + 8 ，也可以是 1 + 3 + 6，甚至可以是 5.5 + 4.4+ 0.1 等等等等……波形也是一樣，同樣的合成波形，可以有無數諧波組合。所以說，效果器根本不能分清楚這些諧波的個數與振幅類型。不過均衡的發明者很聰明，他並不讓 EQ 處理不可琢磨的諧波去改變音色，而是通過一種巧妙的方法，間接的改變了音色。

從高中物理書上的“振動與波”一章可知頻率等於周期的倒數。而所謂周期，就是指物體完成某種運動，回到初始狀態所經歷的時間。

由縱軸的零點來看，這個波形的從 0 時刻從 0 振幅開始跨越 1/440 秒后回到了初始狀態（第 1/880 點縱軸位置也是 0 點，但是運動方向與初始位置相反。所以不能當作返回）。現在我們知道這個波形的頻率是 440Hz（1/440 的倒數），可是這個波形就只有 440Hz 的聲音么？不是的。如果我們從圖中縱軸的某個非零位置看上去。

正如大徠家看到的，這一段里，振動回到平衡位置經歷的時間是 1/1000 秒，也就是說，綠色部分是頻率為 1000Hz 的波形。同樣的，從縱軸不同的非零位置看，可以得到各種頻率的波形。

這樣，我們就近似得到了波形的各個分波。下面 EQ 所要做的，就是調整各個近似分波的振幅（音量）大小。但在這之前，我們先要下一個定義：同樣的波形，在縱軸的不同位置看上去有不同的頻率，我們把從平衡位置（縱軸零點）看上去呈現的頻率稱為“樂音頻率”，把從縱軸不同位置看上去的分波統稱“聲音頻率”。人耳在接收聲音的時候，會自動把耳膜在平衡位置的振動頻率（也就是“樂音頻率”）當作音高，把其他頻率轉化為音色。

模擬 EQ，數字 EQ 橫縱比：最原始的 EQ，是利用電容器的所謂“容抗”現象來調整聲音的音色，所謂“容抗”，既是說電容器有這樣一種物理現象。對於不同規格的電容，其對不同頻率交流電信號有減弱或提升的現象。聲音從 MIC（麥克風）轉化後會變成交流電信號，電流 I 會正比於聲音振幅（其實只能近似正比）。I 通過導線進入 EQ，我們用一個 3 段 EQ 的理論電路來舉例：

3 個不同規格的電容器分別負責調整高頻，中頻和低頻。由於三個電容分別對高、中、低頻率的敏感程度不一樣，人們便可以通過調整各個電容的電流傳輸效率來產生 EQ 效果。這種利用物理現象的方法是明智又省力的，而且相當精確！但是隨著數碼錄音技術的發展，錄音師們開始喜歡在後期加入 EQ，傳統 EQ 便不能滿足需要了。於是越來越多的數字 EQ 出現在了人們眼前。在聲音信號已經量化的數字信號中調整 EQ，就必須利用數學演演算法來解決。大家一定都聽說過“採樣率”這個概念。在數字音頻信號中，波形的變化不能是連續的，而是由一個一個採樣點串起來的。

這種設計產生了一個麻煩——我們在分析採樣點頻率時很難找到另一個採樣點剛好與這個點振幅狀態一致：

所以，數碼 EQ 必須像穿線一樣將各個採樣點連起來，才能近似找到兩個狀態一致的點。說起來容易作起來難，電腦不是人腦，只能以數學方法來“穿線”。最古老的方法，我稱作“直線路徑”即用直線連接各個採樣點。這種做法很簡單，但是誰都知道採樣點與採樣點之間不可能是直線連接，這樣會產生很大誤差！後來人們根據高數中的某個算式（名字忘了），用最接近原始波形的曲線連接了採樣點，我稱作“模擬路徑”。如圖：

這種方法誤差依然存在，畢竟那是理論算出來的不是真正的波形。但是已經與原始波形相差很少很少了。現今流行的數字 EQ，大都採用這種設計。

數字 EQ 的原理：

數字 EQ 雖然種類繁多，其實原理都是一樣的，即：將輸入信號“x”建立對應輸出信號“Y”，Y=f（X），其中 f（）這個作用式中又包括了一個與“x”對應頻率“k”的函數。將對應“X”的函數表達式展開也就是：Y=g（k）*X。其中g（）隨EQ參數調節而變化。

舉例：古老數字 EQ 的原理。

這是一個古老的 3 段 EQ，使用“直線路徑”。我們把中頻提升到 2 倍，高頻提升 3 倍。這時，函數的作用式就變成了：

Y=1*X（k 屬於 0Hz 到 400Hz）

Y=2*X（k 屬於 400Hz 到 2500Hz）

Y=3*X（k 屬於 2500Hz 到無窮）

可以看出，這種 EQ 調節“有塄有角”，399.9Hz 振幅還一點不變，到 401Hz 就突然增加 2 倍。加入了這 EQ，產生了魔鬼的聲音…………現今的 EQ 不但擁有“模擬路徑”，還擁有漸變的函數作用式。同樣的 3 段 EQ，把中頻提升到 2 倍，高頻提升 3 倍，函數圖像會變的很圓滑。

這個“樓梯”很圓滑，在雖然中頻從 400Hz 開始算起，但是從 350Hz 左右就已經開始增加振幅產生漸變的效果。大家可以試試，即便把 EQ 的高頻降低到 0，我們依然可以聽到一點高頻。而且由於採用了“模擬路徑”，使頻率的分析更準確！更加容易調節。但這兩種優化演演算法比古老 EQ 更費系統資源。

我們之所以要講到已經沒有用的古老 EQ，是因為它更方便人們理解 EQ。有些朋友總是問：EQ 效果器既然能改變聲音的頻率，C 調的歌調完 EQ 會不會變成降 B？？降低 bass（低音）的低頻，bass 聽起來會不會好像升了一個 8 度？大家還記得前文提到的“樂音頻率”和“聲音頻率”概念么？我們帶著這個概念從古老 EQ 入手來解釋這兩個問題。

我們來看古老 EQ 的公式：Y=r*X（k屬於a Hz 到 b Hz）。前面已經說過，聲音的音高只與“樂音頻率”有關。也就是說，想證明 EQ 效果器能改變聲音的頻率而不改變音高，只需證明 EQ 效果器能改變聲音頻率而不改變樂音頻率。

根據樂音頻率的定義，它必然是兩個同樣狀態的0點之間時間長度的倒數（第 1 零點，第 3 零點）。我們設 1 點的時刻為 t1，3 點的時刻為 t2。樂音頻率 f=1/(t2－t1)。我們來證明 t1 時刻或者 t2 時刻不發生變化：對於任意一個輸入信號“x”有輸出信號 Y=r*X（k屬於a Hz到b Hz）。在任意 t 時刻，經過 EQ 處理的信號可以改變為任意值。但是由於 1，3 點的 X 值為 0，所以無論我們如何調整 EQ 參數，Y=r*0=0，所以在 1，3 點，X 值永遠等於 Y 值為 0。即所有振幅為 0的時刻點經過 EQ 處理，振幅依然為 0，所以第 1 零點，第 3 零點之間的時間間隔不隨參數變化而變化。

這就是 EQ 效果器能改變聲音頻率而不改變音高的原因，所以大家（尤其是初學者）大可放心地使用 EQ。其實隨著技術的進步，數字 EQ 的演演算法也開始變得多種多樣。就在這篇稿子即將完成時，又聽說有通過任意頻點的前後兩點前後兩點計算斜率（就是該點的速度）來確定頻率的新奇高招，但 EQ 的宗旨不變—— 只改變千篇一律的音色。聲音頻率和音樂中440Hz 等等樂音頻率不是一個概念，調低高頻音樂不可能沒了高聲部，bass 也不會因為降低低頻而消失。