採樣信號
採樣信號
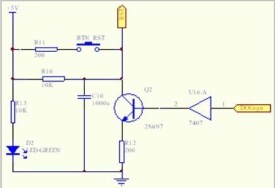
採樣信號,是指模擬信號先由採樣器按照一定時間間隔採樣獲得時間上離散的信號。
示例一
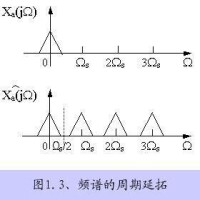
對理想採樣信號進行傅立葉變換,可以證明,理想採樣信號的頻譜是連續信號頻譜的周期延拓,重複周期為(採樣頻率),即
示例二
其中為理想採樣信號的頻譜,為連續信號的付氏變換。顯然,是頻率的連續函數。
數字角頻率。
如果信號是實帶限信號,且最高頻譜不超過,即
採樣定理
那麼理想採樣頻譜中,基帶頻譜以及各次諧波調製頻譜彼此是不重迭的,用一個帶寬為的理想低通濾波器,可以將各次諧波調製頻譜濾除,保留不失真的基帶頻譜,從而不失真地還原出原來的連續信號。
hundie
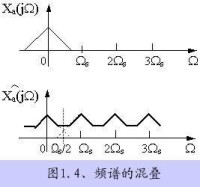
如果信號最高頻譜超過,那麼在理想採樣頻譜中,各次調製頻譜就會互相交疊,出現頻譜的“混淆”現象,如圖1.4。為簡明起見,圖中將作為標量處理,一般為複數,交疊也是複數相加。當出現頻譜混淆后,一般就不可能無失真地濾出基帶頻譜,用基帶濾波恢復出來的信號就要失真。
因此,稱採樣頻率的一半為摺疊頻率,它好像一面鏡子,信號頻譜超過它時,就會被折迭回來,造成頻譜混淆。
奈奎斯特採樣定理:要使實信號採樣后能夠不失真還原,採樣頻率必須大於信號最高頻率的兩倍,即。
實際工作中,為避免頻譜混淆,採樣頻率總是選得比兩倍信號最高頻率更大些,如。同時,為避免高於摺疊頻率的雜散頻譜進入採樣器造成頻譜混淆,採樣器前常常加一個保護性的前置低通濾波器(抗混疊濾波),阻止高於頻率分量進入。
3)採樣信號的拉氏變換
理想採樣后,信號的拉氏變換在S平面上沿虛軸周期延拓,也即在S平面上的虛軸上是周期函數。
在信息處理領域,採樣信號是指模擬信號先由採樣器按照一定時間間隔採樣獲得時間上離散的信號。
這些信號再經模數轉換器(ADC)在數值上也進行離散化,從而得到數值和時間上都離散的數字信號。
整個過程稱之為採樣,很多情況下所說的“採樣”就是指這種採樣與量化結合的過程。
採樣也稱抽樣,是信號在時間上的離散化,即按照一定時間間隔在模擬信號上逐點採取其瞬時值。它是通過採樣脈衝和模擬信號相乘來實現的。
採樣間隔的選擇和信號混淆:對模擬信號採樣首先要確定採樣間隔。如何合理選擇△t涉及到許多需要考慮的技術因素。一般而言,採樣頻率越高,採樣點數就越密,所得離散信號就越逼近於原信號。但過
高的採樣頻率並不可取,對固定長度的信號,採集到過大的數據量(),給計算機增加不必要的計算工作量和存儲空間;若數據量()限定,則採樣時間過短,會導致一些數據信息被排斥在外。採樣
頻率過低,採樣點間隔過遠,則離散信號不足以反映原有信號波形特徵,無法使信號復原,造成信號混淆。
直觀地說信號混迭是把本該是高頻的信號誤認為低頻信號。