低通濾波
低通濾波
低通濾波(Low-pass filter) 是一種過濾方式,規則為低頻信號能正常通過,而超過設定臨界值的高頻信號則被阻隔、減弱。但是阻隔、減弱的幅度則會依據不同的頻率以及不同的濾波程序(目的)而改變。它有的時候也被叫做高頻去除過濾(high-cut filter)或者最高去除過濾(treble-cut filter)。低通過濾是高通過濾的對立。
低通濾波可以簡單的認為:設定一個頻率點,當信號頻率高於這個頻率時不能通過,在數字信號中,這個頻率點也就是截止頻率,當頻域高於這個截止頻率時,則全部賦值為0。因為在這一處理過程中,讓低頻信號全部通過,所以稱為低通濾波。
低通過濾的概念存在於各種不同的領域,諸如電子電路,數據平滑,聲學阻擋,圖像模糊等領域經常會用到。
在數字圖像處理領域,從頻域看,低通濾波可以對圖像進行平滑去噪處理。
對於不同濾波器而言,每個頻率的信號的減弱程度不同。當使用在音頻應用時,它有時被稱為高頻剪切濾波器,或高音消除濾波器。

低通濾波器的幅頻
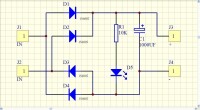
最簡單的濾波電路
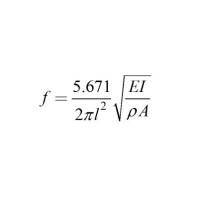
低通濾波
臨界頻率計算公式:
常用的濾波電路有無源濾波和有源濾波兩大類。若濾波電路元件僅由無源元件(電阻、電容、電感)組成,則稱為無源濾波電路。無源濾波的主要形式有電容濾波、電感濾波和複式濾波(包括倒L型、LC濾波、LCπ型濾波和RCπ型濾波等)。若濾波電路不僅有無源元件,還有有源元件(雙極型管、單極型管、集成運放)組成,則稱為有源濾波電路。有源濾波的主要形式是有源RC濾波,也被稱作電子濾波器。
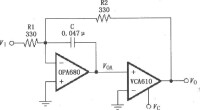
低通濾波電路
無源濾波電路的結構簡單,易於設計,但它的通帶放大倍數及其截止頻率都隨負載而變化,因而不適用於信號處理要求高的場合。無源濾波電路通常用在功率電路中,比如直流電源整流后的濾波,或者大電流負載時採用LC(電感、電容)電路濾波。
有源濾波電路的負載不影響濾波特性,因此常用於信號處理要求高的場合。有源濾波電路一般由RC網路和集成運放組成,因而必須在合適的直流電源供電的情況下才能使用,同時還可以進行放大。但電路的組成和設計也較複雜。有源濾波電路不適用於高電壓大電流的場合,只適用於信號處理。
根據濾波器的特點可知,它的電壓放大倍數的幅頻特性可以準確地描述該電路屬於低通、高通、帶通還是帶阻濾波器,因而如果能定性分析出通帶和阻帶在哪一個頻段,就可以確定濾波器的類型。
識別濾波器的方法是:若信號頻率趨於零時有確定的電壓放大倍數,且信號頻率趨於無窮大時電壓放大倍數趨於零,則為低通濾波器;反之,若信號頻率趨於無窮大時有確定的電壓放大倍數,且信號頻率趨於零時電壓放大倍數趨於零,則為高通濾波器;若信號頻率趨於零和無窮大時電壓放大倍數均趨於零,則為帶通濾波器;反之,若信號頻率趨於零和無窮大時電壓放大倍數具有相同的確定值,且在某一頻率範圍內電壓放大倍數趨於零,則為帶阻濾波器。
有許許多多不同頻率響應的不同類型濾波器電路。濾波器的頻率響應通常用波德圖表示。
例如,一階濾波器在頻率增加一倍(增加octave)時將信號強度減弱一半(大約-6dB)。一階濾波器幅度波特圖在截止頻率之下是一條水平線,在截止頻率之上則是一條斜線。在兩者邊界處還有一個"knee curve"在兩條直線區域之間平緩轉換。參見RC電路。二階濾波器對於削減高頻信號能起到更高的效果。這種類型的濾波器的波特圖類似於一階濾波器,只是它的滾降速率更快。例如,一個二階的巴特沃斯濾波器(它是一個沒有尖峰的臨界衰減RLC電路)頻率增加一倍時就將信號強度衰減到最初的四分之一(每倍頻-12dB)。其它的二階濾波器最初的滾降速度可能依賴於它們的Q因數,但是最後的速度都是每倍頻 -12dB。參見RLC電路。三階和更高階的濾波器也是類似。總之,最後n階濾波器的滾降速率是每倍頻6ndB。
對於任何的巴特沃斯濾波器,如果向右延長水平線並且向左上延伸斜線(函數的漸近線,它們將相交在“截止頻率”。一階濾波器在截止頻率的頻率響應是水平線下-3dB。不同類型的濾波器——巴特沃斯濾波器、切比雪夫濾波器等——都有不同形狀的“knee curves”。許多二階濾波器設計成有“峰值”或者諧振以得到截止頻率處的頻率響應處在水平線之上。參見電子濾波器中其它類型的濾波器。
'低'和'高'的含義——例如截止頻率—— 依賴於濾波器的特性。(術語“低通濾波器”僅僅是指濾波器響應的形狀。一個高通濾波器能夠設計成比任何低通濾波器截止頻率更低的截止頻率。不同的頻率響應是區分它們的依據。)電子濾波器能夠設計成任何所期望的頻率範圍——可以到微波頻率(超過 1000 MHz)乃至更高。
