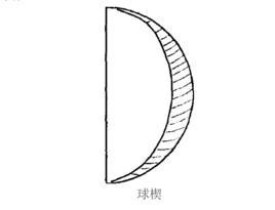
球楔
球楔
球楔(spherical wedge)是過同一直徑的兩個平面,把球分成的一部分(共四個),即以球面月形為底、兩個大圓的半圓面所夾的球體部分(球面月形是指球面上具有同一直徑的兩個大圓的半圓周所夾的球面部分)。這兩個大圓(所在平面)的夾角(即球面角),就是球楔的夾角。當球面角為360°時,球楔就成為球體。
球楔亦稱球劈,是一種與球有關的幾何體。用球的兩個大圓面把球分成四部分,每一部分都稱為球楔。一個球楔的表面由兩個半圓和一部分球面組成,球面部分稱為球楔的底面,是球面二角形。兩半圓面所夾的二面角稱為球楔的角。有的書籍也稱球扇形為球楔。
當球半徑為R,球楔的角為α弧度時,球楔的底面積S=2αR²,體積V=2αR³/3,該球楔的角為2α球面度=α/2π球面角(1球面角=4π球面度) 。
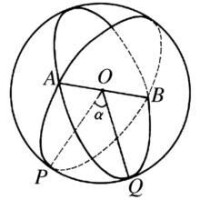
圖1
有的書籍也稱球扇形為球楔。
在半圓內的一個扇形,繞著半圓直徑所在的直線旋轉一周所得到的幾何體叫做球扇形,球扇形可以看作是由一個球帶和兩個圓錐面圍成的或由一個球冠和一個圓錐面所圍成的,這裡的球帶或球冠叫做球扇形的底面,圓錐面叫做球扇形的側面。
球扇形是球的一部分,一個頂點在球心的旋轉圓錐面把球體截成兩部分,每一部分都稱為球扇形,用兩個頂點在球心,共軸而不相等的旋轉圓錐面把球體截成三部分,每一部分也稱為球扇形,將一個不足半圓的圓扇形,繞一條在扇形平面上的過圓心而不穿過扇形內部的直線旋轉,也可生成球扇形,扇形圓弧旋轉所得到的球冠或球帶稱為球扇形的底面,這個球冠或球帶的高稱為球扇形的高,扇面的半徑旋轉生成的圓錐側面稱為球扇形的側面,當旋轉軸與扇形有一直邊重合時,生成的球扇形稱為簡單球扇形,亦稱球面圓錐。否則稱為中空球扇形。
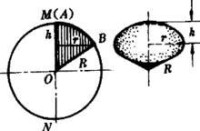
圖2
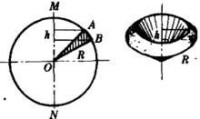
圖3
球扇形(球楔)的體積計算:
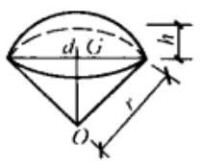
圖4
球楔
球楔
球楔