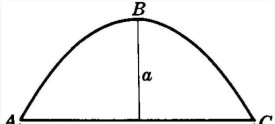
弓形
弓形
弓徠形:由弦及其所對的弧組成的圖形叫做弓形。弦AB把圓分成兩部分,這兩部分都是弓形.弓形是最簡單的組合圖形.當弓形的弧小於半圓時,術語名稱為“優弧弓”,其面積等於扇形面積與三角形面積的差;nπr^2/360-ad/2當弓形的弧大於半圓時,術語名稱為”劣弧弓“,其面積等於扇形面積與三角的面積的和:nπr^2/360+ad÷2當弓形弧是半圓時,術語名稱為”半圓弓“,其面積是圓面積的一半.
弓形:由弦及其所對的弧組成的圖形叫做弓形.

弓形
弦AB把圓分成兩部分,這兩部分都是弓形.弓形是一個最簡單的組合圖形之一.
當弓形的弧小於半圓時,弓形的面積等於扇形面積與三角形面積的差;
當弓形的弧大於半圓時,它的面積等於扇形面積與三角的面積的和;
當弓形弧是半圓時,它的面積是圓面積的一半.
弓
bow;
弓
gōng
(1)
(象形。甲骨文字形,象弓形,有弓背和弓弦,后省去弓弦,只剩下弓背,隸變后變成現在的“弓”字。“弓”是漢字部首之一,從“弓”的字多與“弓箭”有關係。本義:射箭或打彈的器械)
(2)
同本義 [bow]
弓,兵也,所以發矢。――《說文》
弓,揉木而弦之以發矢。――《正字通》
帶長劍兮挾秦弓,首身離兮心不懲。――《楚辭·九歌·國殤》
良冶之子,必學為裘;良弓之子,必學為箕。――《禮記·學記》
毋弛而弓,一棲兩雄。――《韓非子·揚權》
胡人不敢南下而牧馬,士不敢彎弓而報怨。――漢·賈誼《過秦論》
一代天驕,成吉思汗,只識彎弓射大雕。――毛澤東《沁園春·雪》
(3)
又如:弓手(亦作“弓箭手”。宋元時州縣統轄的負責巡邏、緝捕的兵卒);弓壺(有“弓”字銘文的酒器;裝弓的袋);弓號(弓);弓劍(弓與劍);弓箕(弓和箕。喻指世傳的家業技藝)
(4)
形狀或作用像弓的器具 [anything bow-shaped]
忽然翻出一雙繡花的弓鞋來。――《范愛農》
劍花寒不落,弓月曉逾明。――《樂府詩集·隋·明餘慶·軍行》
(5)
又如:彈弓;胡琴弓;弓小(弓形而纖小);弓彎(弓鞋。指纏腳婦女穿的鞋)
(6)
演奏弓弦樂器時的運弓技術 [bowing]。如:連弓;分弓;頓弓;連頓弓;擊跳弓;彈跳弓;拋弓
(7)
丈量土地的器具,用木製成,形狀似弓 [old unit for measuring length of land(=5尺)],兩端距離是五尺,也叫步弓
侯道五十弓。――《儀禮·鄉射禮記》
丈地弓制不真,責之弓手。――清·黃六鴻《清文部·責經手》
(8)
又如:弓手(古代丈量地畝持步弓的人)
弓
gōng
〈量〉
(1)
丈量土地的計量單位,一弓為五尺、三百六十弓為一里 [a measure of length]
自冢至麓,凡二百弓。――唐·陸龜蒙《送小雞山樵人序》
(2)
又如:弓口(尺寸。弓:丈量土地的計量單位)
弓
gōng
(1)
彎曲,引申為彎身,指行禮 [bend;bow]
據唐·段成式《酉陽雜俎·諾皋記》載,謂有士人醉卧,見婦人踏歌曰:“舞袖弓腰渾忘卻,蛾眉空帶九秋霜。”其中雙鬟者問如何是弓腰?歌者笑曰:“汝不見我作弓腰乎?”乃返首髻及地,腰勢如規
(2)
又如:弓腰人(古指舞伎);弓身
弓箭步
gōngjiànbù
[Bow-and-Arrow Step] 是丁字步的一種變形和發展,它是將丁字步的前腿向旁伸出后彎曲,後腿綳直,即前腿弓,後腿直。弓的腿足尖向正旁,直的腿足尖向正前。弓的腿要求小腿和地面成垂直角度,大腿和小腿成稍大於90暗畝勱?重心在兩腿中間,上身直立,方向對正前,雙肩要和腿在一平面上,頭可看正前,也可看前側
弓箭手
gōngjiànshǒu
[archer] 常常帶有西徐亞人徠血統的古代雅典的公共奴隸,身備弓箭,並且擔任警察;古代專司射箭的士兵
弓弩
gōngnǔ
[bow and arrow] 弓和弩
弓弩手
弓弩手
gōngnǔshǒu
[crossbowman] 以弩弓為武器的人(如兵士或獵人)
弓身
gōngshēn
[bend] 彎下身子
弓身哈腰
弓弦,弓弦兒
gōngxián,gōngxiánr
(1)
[bowstring]∶弓上的弦
(2)
[straightaway]∶比喻比彎道短而直的路線
順著小路走,凈走弓弦,近便多了
射者,弓弦發矢也。――《管子·形勢》
弓形
gōngxíng
[segment of a circle] 圓弧和它所對的弦圍成的圖形
弓腰
gōngyāo
[hunch] 向後彎腰及地如弓形
弓
gōngㄍㄨㄥˉ
(1)
射箭或發彈丸的器具:~箭。~弩。飛鳥盡,良~藏。
(2)
像弓的器具或形態:胡琴~子。~鞋。
(3)
舊時丈量地畝用的器具和計算單位。
(4)
彎曲:~身。
(5)
姓。
鄭碼:YZ,U:5F13,GBK:B9AD
筆畫數:3,部首:弓,筆順編號:515
bow;
S=1/2R²(θ-sinθ)
=1/2 [R^2θ-b(R-h)]
=1/2(R^2θ-b√(R^2-h^2/4))
≈2/3bh (θ越小,誤差越小)
b=2Rsin(θ/2)
R=(b^2+4h^2)/8h
θ=4arctan(2h/b)
h=2Rsin^2(θ/4)
=1/2btan(θ/4)
=R-Rcos(θ/2)
[R為弓形所在圓的半徑,θ為弧所對圓心角,h為矢高(即弓形的高),b為弦長]
設弓形AB所對的弧為弧AB,那麼:
當弧AB是劣弧時,那麼S弓形=S扇形-S△AOB(A、B是弧的端點,O是圓心)。
當弧AB是半圓時,那麼S弓形=S扇形=1/2S圓=1/2×πr²。
當弧AB是優弧時,那麼S弓形=S扇形+S△AOB(A、B是弧的端點,O是圓心)
計算公式分別是:
S=nπR²/360-ah/2
S=πR²/2
S=nπR²/360+ah/2
(n為弧度,R為半徑,a為弦長,h為三角形的高)加一個/是分數線
已知一個弧形的弧長8.20m,高為1.75m,底寬7.30m,求弓形的面積。
解:
已知弧長L=8.20m,設扇形半徑為r,
由勾股定理有r²=(7.30/2)²+(r-1.75)²,解得r=4.6814m
所以
扇形面積=0.5Lr=0.5*8.20*4.6814=19.1937
三角形面積=0.5*7.30(r-h)=0.5*7.30*(4.6814-1.75)=10.6996
所以弓形面積=扇形面積-三角形面積=19.1937-10.6996=8.494
球台是指球體被兩個平行平面所截而夾在兩平面中間的部分。截得的兩個圓面分別為上底和下底,垂直於圓面的直徑被截得的部分是高。
球台的體積:
r1,r2為球台的上、下底半徑,h為球台的高
S1,S2為球台的上、下底面積,h為球台的高
圓錐曲線,又稱圓錐截痕、圓錐截面、二次平面曲線,是數學、幾何學中通過平切圓錐(嚴格為一個正圓錐面和一個平面完整相切)得到的曲線,包括圓,橢圓,拋物線,雙曲線及一些退化類型。
圓錐曲線在約公元前200年時就已被命名和研究了,其發現者為古希臘的數學家阿波羅尼奧斯,那時阿波羅尼阿斯對它們的性質已做了系統性的研究。
圓錐曲線應用最廣泛的定義為(橢圓,拋物線,雙曲線的統一定義):動點到一定點(焦點)的距離與其到一定直線(準線)的距離之比為常數(離心率e)的點的集合是圓錐曲線。對於0 1得到雙曲線 。