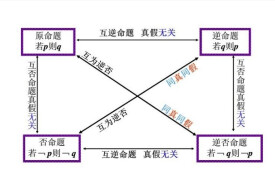
假命題
假命題
如果一個命題的題設成立時,不能保證結論一定成立,那麼這樣的命題叫做假命題。
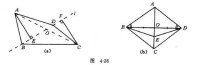
命題及其表示法
②那麼.
③頂角.
公理是人們在長期實踐中總結出來的、正確的命題,它不需要用其他的方法來證明,初一幾何中我們過的主要公理有:
①經過兩點有一條直線,並且只有一條直線.
②經過直線外一點有且只有一條直線與這條直線平行.
③同位角相等,兩直線平行.
④兩直線平行,同位角相等.
假命題
如:
三角形的三個內角和不等於180度。
一個命題都可以寫成這樣的格式:如果+題設,那麼+結論。
對於其中所有背景,所陳述的情況都不屬實的命題是假命題。
如:
三角形的三個內角和不等於180度。
人會飛。
對於其中若干背景,所陳述的情況不屬實的命題,即使對於另外若干背景,所陳述的情況屬實,也是假命題。
如:
菱形是長方形(菱形中只有是正方形的菱形才是長方形)。
另外有些命題的條件和結論互換,效果是不一樣的,有的可能從真命題變成假命題,有的可能性質不變,如:
對頂角是相等的角(真)
相等的角是對頂角(假)
長方形是菱形。(假)
菱形是長方形。(假)
內角和為180度的多邊形是三角形。(真)
三角形是內角和為180度的多邊形。(真)
假命題可分為三類情況:
1.題設只對應一種背景,且結論是錯誤的。例如,“”就是一個假命題。
2.題設對應多種背景,且對於其中所有背景,結論都是錯誤的。例如“兩直線平行,同旁內角互余”,這一命題的題設對應多種背景:對於其中所有背景,同旁內角都是互補而不是互余的。這個命題是一個假命題。
3. 題設對應多種背景,對於其中若干背景,結論是錯誤的,但對於另外若干背景,結論是正確的。例如“兩條直線平行,同旁內角相等”這一命題的題設對應多種背景:對於其中一堆背景,同旁內角的一個角大於90°,另一個角小於90°,同旁內角不相等;但是對於另外一種背景,同旁內角的兩個角都等於90°,同旁內角相等。如此,這一命題的題設對應的所有背景中,對於其中一堆背景,結論是錯誤的。這一命題是假命題。