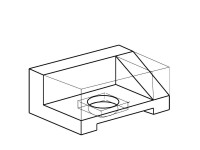
正等軸測圖
正等軸測圖
將形體放置成使它的三條坐標軸與軸測投影面具有相同的夾角(35°16′),然後向軸測投影面作正投影。用這種方法作出的軸測圖稱為正等軸測圖。
將形體放置成使它的三條坐標軸與軸測投影面具有相同的(120°)夾角,然後向軸測投影面作正投影。用這種方法作出的軸測圖稱為正等軸測圖。
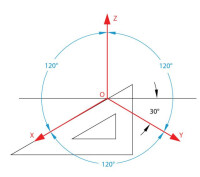
正等軸測圖
軸測投影的形成
將物體連同其直角坐標體系,沿不平行與任一坐標平面的方向,用平行投影法將其投射在單一投影面上所得到的圖形,稱為軸測投影(軸測圖),如圖7-2a 、b中投影P上所得到的圖形。
軸測投影被選定的單一投影P,稱為軸測投影面。直角坐標軸OX、OY、OZ在軸測投影P上的軸測投影OX、OY、OZ,稱為軸測投影軸,簡稱軸測軸。
直角坐標體系 由三根相互垂直的軸(直角坐標軸)和相同的原點及其計量單位所構成的坐標體系。
坐標體系 確定空間每個點及其相應位置之間關係的基準體系。
直角坐標軸 在直角體系中垂直相交的坐標軸。
坐標平面 任意兩根坐標軸所確定的平面。
原點 坐標軸的基準點。
軸測投影也屬於平行投影,且只有一個投影面。當確定物體的三個坐標平面不與投射方向一致時,則物體上平行於三個坐標平面的平面圖形的軸測投影,在軸測投影面上都得到反映,因此,物體的軸測投影才有較強的立體感。
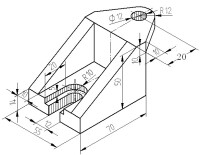
軸測圖
軸間角和軸向伸縮係數
1.軸間角
軸測投影中任意兩根直角坐標軸在軸測投影面上的投影之間的夾角,稱為軸間角。如圖5-2所示,兩軸側軸之間夾角(∠XOY、∠XOZ、∠YOZ),用它來控制軸測投影的形狀變化。
2. 軸向伸縮係數
直角坐標軸的軸測投影的單位長度,與相應直角坐標軸上的單位長度的比值,稱為軸向伸縮係數,如圖所示,其中,用p表OX軸軸向伸縮係數,q表示OY軸軸向伸縮係數,r表示OZ軸軸向伸縮係數,用軸向伸縮係數控制軸測投影的大小變化。
軸測投影的基本性質
軸測投影同樣具有平行投影的性質:
(1)若空間兩直線段相互平行,則其軸測投影相互平行。
(2)凡與直角坐標軸平行的直線段,其軸測投影必平行於相應的軸測軸,且其伸縮係數於相應軸測軸的軸向伸縮係數相同。因此,畫軸測投影時,必沿軸測軸或平行於軸測軸的方向才可以度量。軸測投影因此而得名。
(3)直線段上兩線段長度之比,等於其軸測投影長度之比。
軸測投影的分類
按獲得軸測投影的投射方向對軸測投影面的相對位置不同,軸測投影可分為兩大類:
1.正軸測投影
用正投影法得到的軸測投影,稱為正軸測投影。
2.斜軸測投影
用斜投影法得到的軸測投影,稱為斜軸測投影。
由於確定空間物體位置的直角坐標軸對軸測投影面的傾角大小不同,軸向伸縮係數也隨之不同,故上述兩類軸測投影又個分為三種:
正軸測投影分為:
(1)正等軸測投影(正等軸測圖)
三個軸向伸縮係數均相等(p= q=r)的正軸測投影,稱為正等軸測投影(簡稱正等測)。
(2)正二等軸測投影(正二軸測圖)
兩個軸向伸縮係數相等(p=q≠r或p=r≠q或q=r≠p)的正軸測投影,稱為正二等軸測投影(簡稱正二測)。
(3)正三軸測投影(正三軸測圖)。
三個軸向伸縮係數均不相等(p≠q≠r)的正軸測投影,稱為正三軸測投影(簡稱正三測)。
斜軸測投影分為:
(1)斜等軸測投影(斜等軸測圖)
三個軸向伸縮係數均相等(p=q=r)的斜軸測投影,稱為斜等軸測投影(簡稱斜等測)。
(2)斜二等軸測投影(斜二軸測圖)
軸測投影面平行一個坐標平面,且平行於坐標平面的兩根軸的軸向伸縮係數相等(p=q≠r或p=r≠q 或q=r≠p)的斜軸測投影,稱為斜二等軸測投影(簡稱斜二測)。
(3)斜三軸測投影(斜三軸測圖)
三個軸向伸縮係數均不等(p≠q≠r)的斜軸測投影,稱為斜三軸測投影(簡稱斜三測)。
在實際工作中,正等測、斜二等測用得交多,正(斜)三測的作圖較繁,很少採用。本章只介紹正等測和斜二測的畫法。
正等軸測投影的形成
正等軸測投影的投射方向S垂直於軸測投影間P,如圖 a所示,且確定物體空間位置的三個坐標平面與軸測投影面均傾斜,其上的三根直角坐標軸與軸測投影面的傾角均相等,物體上平行於三個坐標平面的平面圖形的正等軸測投影的形狀和大小的變化均相同,因此,物體的正等軸投影的立體感頗強。
正等軸測投影的軸間角和軸向伸縮係數
1、軸間角
正等軸測圖
正等軸測投影中OX、OY、OZ軸的軸向伸縮係數相等,即 p=q=r。經數學推導得:p=q=r≈0.82。為作圖方便,取簡化軸向伸縮係數p=q=r=1,這樣,畫出的圖形,在沿各軸向長度上均分別放大到1/0.82≈1.22倍,如圖c所示。
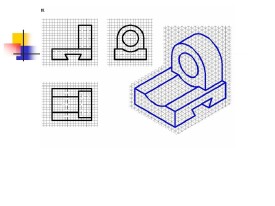
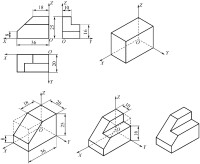
平面立體的正等軸測圖畫法
基本方法是按坐標畫出各頂點的軸測圖,稱為坐標法,見右圖
兩例。
曲面立體的正等軸測圖的畫法
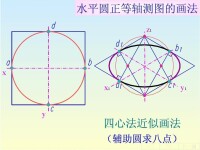
曲面立體的正等軸測圖的畫法實例