幾何定理
幾何定理
幾何定理，屬於數學領域。分為平面幾何、解析幾何。具體事例有勾股定理餘弦定理。條目分為立體幾何，三角形的六心以及重要定理等。
目錄
平面幾何：
線
平行線判定定理
平行線性質定理
垂直平分線
平行線分線段成比例定理
角
角平分線定理
角平分線長公式
分角定理
等角定理
三代角定理
三角形的定理
重心
垂心
內心
外心
旁心
三角形五心定律
九點圓圓心
費馬點
布洛卡點
葛爾剛點
歐拉點
歐拉線
歐拉圓（九點圓）
歐拉定理
三角形內角和定理
三角形中位線定理
SSS
SAS
ASA
AAS
HL
等角對等邊
等邊對等角
大角對大邊
大邊對大角
三線合一
正弦定理
餘弦定理
正切定理
餘切定理
梅涅勞斯定理（及其逆定理）
塞瓦定理（及其逆定理）
中線定理
斯台沃特定理
拿破崙定理
海倫公式
清宮定理
愛爾可斯定理
迪沙格定理
費爾巴哈定理
燕尾定理
波朗傑、騰下定理
卡諾定理
奧倍爾定理
他拿定理
康托爾定理
直角三角形的定理
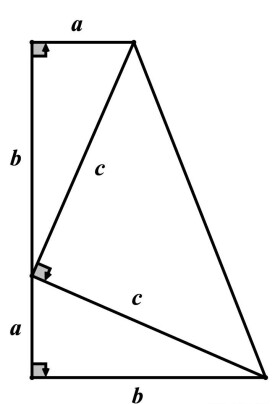
勾股定理(畢達哥拉斯定理）
勾股數勾股方程
射影定理（歐幾里得定理）
直角三角形斜邊中線定理
四邊形的定理
多邊形內角和定理
平行四邊形性質定理
平行四邊形判定定理
矩形性質定理
矩形判定定理
菱形性質定理
菱形判定定理
菱形面積公式
正方形性質定理
正方形判定定理
等腰梯形判定定理
等腰梯形性質定理
梯形蝴蝶定理
牛頓定理
芬斯勒–哈德維格爾定理
泰博定理
馮奧貝爾定理
密克爾點
圓：
垂徑定理
圓周角定理
弦切角定理
切線長定理
切割線定理
割線定理
相交弦定理
圓冪定理
西姆松定理
托勒密定理
蝴蝶定理
婆羅摩笈多定理
根心定理
三圓定理
四圓定理
五圓定理
坎迪定理
三弦共點定理
雞爪定理
沢山定理
開世定理
史坦納定理
三弦定理
密克定理
共圓定理
朗古來定理
曼海姆定理
巴斯卡定理
安寧定理
布利安松定理
巴斯加定理
射影幾何：
帕斯卡定理
布列安桑定理
交比定理
帕普斯定理
笛沙格定理
解析幾何：
兩點間距離公式
定比分點公式
中點公式
平行線間的距離公式
點到直線的距離公式
點動論
幾何圖形的矢量化原理
圖像性質的數式化原理（處理對稱，最短等問題）
平行四邊形定理
棣莫弗定理
變化率放縮原理（由數式的圖像來判定兩個多項式的大小關係）
超弦原理
定積分，牛頓-萊布尼茨公式
立體幾何
直線與平面平行的判定定理
直線與平面平行的性質定理
平面與平面平行的判定定理
平面與平面平行的性質定理
直線與平面垂直的判定定理
直線與平面垂直的性質定理
平面與平面垂直的判定定理
平面與平面垂直的性質定理
異面直線判定定理
三垂線定理
三垂線逆定理
三正弦定理
三餘弦定理
最小角定理
射影面積定理
射影長定理
祖暅原理
基本信息
- 中文名
- 幾何定理
- 外文名
- geometrictheorems
- 學科門類
- 平面幾何、解析幾何
- 應用
- 數學
- 定義
- “幾何定理”分類
- 條目
- 平面幾何、
- 具體示例
- 勾股定理餘弦定理