希爾排序
希爾排序
希爾排序(Shell's Sort)是插入排序的一種又稱“縮小增量排序”(Diminishing Increment Sort),是直接插入排序演演算法的一種更高效的改進版本。希爾排序是非穩定排序演演算法。該方法因D.L.Shell於1959年提出而得名。
希爾排序是把記錄按下標的一定增量分組,對每組使用直接插入排序演演算法排序;隨著增量逐漸減少,每組包含的關鍵詞越來越多,當增量減至1時,整個文件恰被分成一組,演演算法便終止。
希爾排序按其設計者希爾(Donald Shell)的名字命名,該演演算法由1959年公布。一些老版本教科書和參考手冊把該演演算法命名為Shell-Metzner,即包含Marlene Metzner Norton的名字,但是根據Metzner本人的說法,“我沒有為這種演演算法做任何事,我的名字不應該出現在演演算法的名字中。”
希爾排序是基於插入排序的以下兩點性質而提出改進方法的:
插入排序在對幾乎已經排好序的數據操作時,效率高,即可以達到線性排序的效率。
但插入排序一般來說是低效的,因為插入排序每次只能將數據移動一位。
1、插入排序在對幾乎已經排好序的數據操作時,效率高,即可以達到線性排序的效率。
2、但插入排序一般來說是低效的,因為插入排序每次只能將數據移動一位。
先取一個小於n的整數d1作為第一個增量,把文件的全部記錄分組。所有距離為d1的倍數的記錄放在同一個組中。先在各組內進行直接插入排序;然後,取第二個增量重複上述的分組和排序,直至所取的增量 ( …),即所有記錄放在同一組中進行直接插入排序為止。
該方法實質上是一種分組插入方法
比較相隔較遠距離(稱為增量)的數,使得數移動時能跨過多個元素,則進行一次比較就可能消除多個元素交換。D.L.shell於1959年在以他名字命名的排序演演算法中實現了這一思想。演演算法先將要排序的一組數按某個增量d分成若干組,每組中記錄的下標相差d.對每組中全部元素進行排序,然後再用一個較小的增量對它進行,在每組中再進行排序。當增量減到1時,整個要排序的數被分成一組,排序完成。
一般的初次取序列的一半為增量,以後每次減半,直到增量為1。
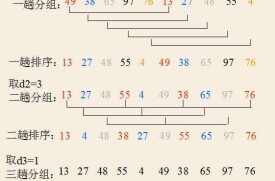
給定實例的shell排序的排序過程
假設待排序文件有10個記錄,其關鍵字分別是:
49,38,65,97,76,13,27,49,55,04。
增量序列的取值依次為:
5,2,1
由於多次插入排序,我們知道一次插入排序是穩定的,不會改變相同元素的相對順序,但在不同的插入排序過程中,相同的元素可能在各自的插入排序中移動,最後其穩定性就會被打亂,所以shell排序是不穩定的。
希爾排序屬於插入類排序,是將整個有序序列分割成若干小的子序列分別進行插入排序。
排序過程:先取一個正整數,把所有序號相隔d1的數組元素放一組,組內進行直接插入排序;然後取,重複上述分組和排序操作;直至,即所有記錄放進一個組中排序為止。
三趟結果
04 13 27 38 49 49 55 65 76 97
Shell排序的演演算法實現:
1. 不設監視哨的演演算法描述
void ShellPass(SeqList R,int d)
{//希爾排序中的一趟排序,d為當前增量
for() //將分別插入各組當前的有序區
if(R[ i ].key
; //R[0]只是暫存單元,不是哨兵
do {//查找R的插入位置
; //后移記錄
; //查找前一記錄
}while(j>0&&R[0].key
; //插入R到正確的位置上
} //endif
不需要大量的輔助空間,和歸併排序一樣容易實現。希爾排序是基於插入排序的一種演演算法,在此演演算法基礎之上增加了一個新的特性,提高了效率。希爾排序的時間複雜度與增量序列的選取有關,例如希爾增量時間複雜度為,而Hibbard增量的希爾排序的時間複雜度為 ,希爾排序時間複雜度的下界是。希爾排序沒有快速排序演演算法快,因此中等大小規模表現良好,對規模非常大的數據排序不是最優選擇。但是比O( )複雜度的演演算法快得多。並且希爾排序非常容易實現,演演算法代碼短而簡單。此外,希爾演演算法在最壞的情況下和平均情況下執行效率相差不是很多,與此同時快速排序在最壞的情況下執行的效率會非常差。專家們提倡,幾乎任何排序工作在開始時都可以用希爾排序,若在實際使用中證明它不夠快,再改成快速排序這樣更高級的排序演演算法. 本質上講,希爾排序演演算法是直接插入排序演演算法的一種改進,減少了其複製的次數,速度要快很多。原因是,當n值很大時數據項每一趟排序需要移動的個數很少,但數據項的距離很長。當n值減小時每一趟需要移動的數據增多,此時已經接近於它們排序后的最終位置。正是這兩種情況的結合才使希爾排序效率比插入排序高很多。演演算法的性能與所選取的分組長度序列有很大關係。只對特定的待排序記錄序列,可以準確地估算關鍵詞的比較次數和對象移動次數。想要弄清關鍵詞比較次數和記錄移動次數與增量選擇之間的關係,並給出完整的數學分析,今仍然是數學難題。
1.增量序列的選擇
Shell排序的執行時間依賴於增量序列。
好的增量序列的共同特徵:
① 最後一個增量必須為1;
② 應該盡量避免序列中的值(尤其是相鄰的值)互為倍數的情況。
有人通過大量的實驗,給出了較好的結果:當n較大時,比較和移動的次數約在到之間。
2.Shell排序的時間性能優於直接插入排序
希爾排序的時間性能優於直接插入排序的原因:
①當文件初態基本有序時直接插入排序所需的比較和移動次數均較少。
②當n值較小時,n和 的差別也較小,即直接插入排序的最好時間複雜度O(n)和最壞時間複雜度0( )差別不大。
③在希爾排序開始時增量較大,分組較多,每組的記錄數目少,故各組內直接插入較快,後來增量逐漸縮小,分組數逐漸減少,而各組的記錄數目逐漸增多,但由於已經按作為距離排過序,使文件較接近於有序狀態,所以新的一趟排序過程也較快。
因此,希爾排序在效率上較直接插入排序有較大的改進。
希爾排序是按照不同步長對元素進行插入排序,當剛開始元素很無序的時候,步長最大,所以插入排序的元素個數很少,速度很快;當元素基本有序了,步長很小,插入排序對於有序的序列效率很高。所以,希爾排序的時間複雜度會比好一些。
input: an array a of length n with array elements numbered 0 to
inc ← round()
while inc > 0 do:
temp ← a[i]
j ← i
while j ≥ inc and a[j − inc] > temp do:
a[j] ← a[j − inc]
j ← j − inc
a[j] ← temp
inc ← round(inc / 2.2)
1 2 3 4 5 6 7 8 9 10 11 12 13 | func ShellSort(nums []int) []int{ //外層步長控制 for step := len(nums) / 2; step > 0; step /= 2 { //開始插入排序 for i := step; i < len(nums); i++ { //滿足條件則插入 for j := i - step; j >= 0 && nums[j+step] < nums[j]; j -= step { nums[j], nums[j+step] = nums[j+step], nums[j] } } } return nums } |
1 2 3 4 5 6 7 8 9 10 | def shell(nums): n = len(nums) gap = n // 2 while gap > 0: for i in range(gap, n): while i >= gap and nums[i - gap] > nums[i]: nums[i - gap], nums[i] = nums[i], nums[i - gap] i -= gap gap //= 2 return nums |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | + (NSArray *)shellSort:(NSArray *)unsortDatas { NSMutableArray *unSortArray = [unsortDatas mutableCopy]; int len = (int)unSortArray.count; for (int gap = floor(len / 2); gap > 0; gap = floor(gap/2)) { for (int i = gap; i < len; i++) { for (int j = i - gap; j >= 0 && [unSortArray[j] integerValue] > [unSortArray[j+gap] integerValue]; j-=gap) { NSNumber *temp = unSortArray[j]; unSortArray[j] = unSortArray[gap+j]; unSortArray[gap+j] = temp; } } } return [unSortArray copy]; } |
目錄