相量法
分析正弦穩態電路的便捷方法
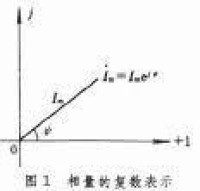
相量法,專業術語,拼音為xiàng liàng fǎ,(phasor method),分析正弦穩態電路的便捷方法。它用稱為相量的複數代表正弦量,將描述正弦穩態電路的微分(積分)方程變換成複數代數方程,從而簡化了電路的分析和計算。該法自1893年由德國人C.P.施泰因梅茨提出后,得到廣泛應用。相量可在複平面上用一個矢量來表示。
相量法

相量法
三角形式∶ A=〡 A〡(Cosθ+jSinθ)
指數形式∶ A=〡 A〡e^jθ
極坐標形式∶ A=〡 A〡∠θ
相量法的代數式和三角形式便於加減運算,指數形式和極坐標形式便於乘除運算。
幅角取值範圍為-π~+π之間。

相量法
相量表示正弦量是指兩者有對應關係,並不是指兩者相等。因為正弦量是時間函數,而相量只是與正弦量的大小及初相相對應的複數。
分析正弦穩態電路的一種方法。1893年由德國人C.P.施泰因梅茨首先提出。此法是用稱為相量的複數來代表正弦量,將描述正弦穩態電路的微分(積分)方程變換成複數代數方程,從而在較大的程度上簡化了電路的分析和計算。目前,在進行分析電路的正弦穩態時,人們幾乎都採用這種方法。
相量法
上式中的Imejψi是一個複數,用符號m表示,稱為正弦量的振幅相量,其值為 夒m=Imejψi=Imcosψi+jImsinψi (2)
用有效代替振幅Im,得到有效值相量夒,其值為 (3) 顯然,在角頻率ω已知的情況下,可以用振幅相量或有效值相量代表一個正弦量。
正弦量與它的相量是一一對應的。給定了正弦量的瞬時值表達式 可以用式中振幅(或有效值)和初相角組成相量
給定了正弦量的瞬時值表達式i(t)=Imsin(ωt+ψi)=√2Isin(ωt+ψi),可以用式中振幅(或有效值)和初相角(Initial phase angle)組成相量(或);給定了相量或,可以利用相量的模和幅角,以及已知的角頻率組成正弦量的瞬時值表達式 i(t)=Imsin(ωt+ψi)=√2Isin(ωt+ψi)。
相量圖
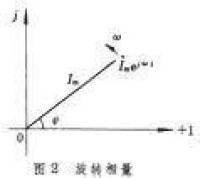
相量是一個複數,複數在複平面上可以用一個矢量來表示,所以一個相量可以用複平面上的一個矢量來表示,如圖1所示。這種表示相量的圖稱為相量圖。若相量乘上ejwt,則表示該相量的矢量以角速度ω繞原點反時針旋轉,於是得到一個旋轉矢量,如圖2所示。這個旋轉矢量稱為旋轉相量,它在任何時刻在虛軸上的投影即為正弦量在該時刻的瞬時值,如圖3所示。相量法
相量法
基爾霍夫定律的相量形式
在正弦穩態下,基爾霍夫定律中的電流和電壓都是正弦量。用相量代表正弦電流和電壓后,基爾霍夫電流定律(KCL)和基爾霍夫電壓定律(KVL)分別變成
∑夒m=0 或 ∑夒=0
∑妧m=0 或 ∑妧=0
電路元件的電壓相量與電流相量的關係
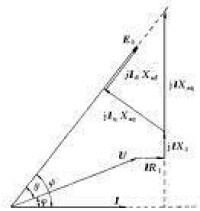
利用相量可將電路元件在時域中的電壓電流關係轉換成電 壓相量與電流相量的關係。正弦電路中幾種常用元件的電壓相量與電流相量的關係如表所示。將正弦交流電路中每個電路均用對應的相量電路模型代替,便得到一個與原電路相對應的相量電路模型,這種模型對正弦交流電路的計算很有用處。相量法
複數阻抗與複數導納
正弦交流電路中一個不含獨立電源且與外電路無耦合的一埠網路,其端上的電壓相量與電流相量的比值定義為該網路的入端複數阻抗,簡稱阻抗。它的倒數定義為該網路的入端複數導納,簡稱導納,分別用符號Z和Y表示。複數阻抗的實部稱為等效電阻,虛部稱為電抗,模稱為阻抗模,幅角稱為阻抗角,它們分別用符號R、X、|Z|、φ表示。複數導納的實部稱為等效電導,虛部稱為電納,模稱為導納模,幅角稱為導納角,它們分別用符號G、B、|Y|、φ┡表示,於是Z =R+jX=|Z|e
Y =G+jB=|Y|e
相量法
用相量法計算正弦交流電路
用此法計算電路有兩種方式,一種方式是,先象暫態分析那樣寫出電路的微分方程,再將方程中的正弦量和對正弦量的運算按規則改換成相量和對相量的運算,得出與原微方程相對應的含相量的代數方程,然後,解此方程求出待求相量。另一種方式,也是通常所用的方式,則是在原電路的相量電路模型上,使用KCL和KVL的相量形式和電路元件電壓-電流關係的相量形式,如同計算直流電路那樣,直接列出含相量的代數方程,然後解此方程求出待求相量。兩種方式得到的解答完全一樣。有了相量便不難寫出原來需要求的正弦量。
