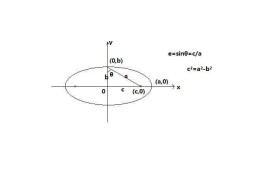
橢圓離心率

偏心率，離心率

eccentricity

離心率統一定義是動點到左（右）焦點的距離和動點到左（右）準線的距離之比。

橢圓扁平程度的一種量度，離心率定義為橢圓兩焦點間的距離和長軸長度的比值，用e表示，即e=c/a (c,半焦距；a,長半軸)

橢圓的離心率可以形象地理解為，在橢圓的長軸不變的前提下，兩個焦點離開中心的程度。

離心率=(ra-rp)/(ra+rp)，ra指遠點距離，rp指近點距離。

圓的離心率=0

橢圓的離心率：e=c/a(0,1)（c,半焦距；a,半長軸(橢圓)/半實軸(雙曲線) ）

拋物線的離心率：e=1

雙曲線的離心率：e=c/a(1,+∞) （c,半焦距；a,半長軸(橢圓)/半實軸(雙曲線) ）

在圓錐曲線統一定義中，圓錐曲線（二次非圓曲線）的統一極坐標方程為

ρ=ep/(1-e×cosθ)，其中e表示離心率，p為焦點到準線的距離。

橢圓上任意一點到兩焦點的距離等於a±ex。

且離心率和曲線形狀對照關係綜合如下：

e=0, 圓

0

e=1, 拋物線

e>1, 雙曲線