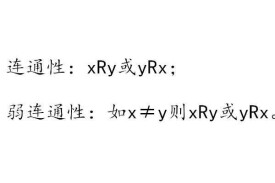連通關係

連通關係是指任意兩個不同的事物之間，與其反關係總有一個成立的那種關係。集合A上的二元關係R，對任何a，b∈A，a≠b有aRb或bRa，用符號表示：R是A上的連通關係 ∀a∀b(a∈A∧b∈A∧a≠b→aRb∨bRa)。當R是A上的連通關係時，稱R在A上是連通的，或稱A上的關係R有連通性。

例如，實數集上的小於關係“<”是連通的，“≤”也是連通的.A上關係R是連通的，當且僅當它把A中任何兩個不相同的元素都聯繫起來。如R的矩陣為M=(r)，則對任何i，j∈λ，i≠j時r與r中至少有一個是1；如R是連通的，則R是連通的，且R∪R 的矩陣主對角線以外的元素全為1；若R，G是連通的，則R∪G也是連通的。

非空集X上的二元關係R，為X中元素所有序對的乘積集合X×X={(x，y)：x,y∈X}的子集，我們寫成xRy(x與y有關係R)，這就是說，(x, y)處於關係R中，同樣，非(xRy)意為(x,y)不是處在關係R中，即x與y沒有關係R 。

二元關係的八種內在屬性，按以下四組關係列出，定義的表示式意即對X所有元素x, y, z都適用，

自反性：xRx；

非自反性：非(xRx)；

對稱性：如xRy，則yRx；

反對稱性：如xRy，則非(yRx)；

傳遞性：如xRy且yRx，則xRz；

負傳遞性：如非(xRy)且非(yRz)，則非(xRz)；

連通性：xRy或yRx；

弱連通性：如x≠y則xRy或yRx。

除了最後兩項，其他都是標準術語，連通性常常稱做 強連通性或 完備性，弱連通性有時也叫做完備性，連通性或弱連通性。這裡，名詞就按以上定義的使用。

第一組兩個性質是相反的(不能同時並存)，但對後面三組就不是這樣。比方說，反對稱和負傳遞性蘊含傳遞性，連通性蘊含弱連通性，而對稱與反對稱僅當R為空集時並存。假如R非空，則對稱性與反對稱性為相反互斥。

設X為所有活人的集合：則“高於”就是非“自反”、反對稱、傳遞的和負傳遞的；“如....一樣老’就是自反的，傳遞的，負傳遞的和連通的；“為.....的姐妹”(至少同父或同母)是對稱的(無傳遞性，為什麼?)，而“知道....的名字”解釋健忘症，對上面八個屬性都不滿足。

傳遞的二元關係稱為序或序關係。可惜，序關係名詞的使用不是一致的。例如，非對稱，傳遞的和弱連通的關係(如在實數集合中的“大於”)，使用著不同的稱呼，如線性序、強序、簡單序、整序、全序、連通序和鏈等名稱，其中有些也用來命名其他特徵定義的序。因之，當提到某一類型的序的時候，重要的是要弄清它的定義特性。