實數
實數
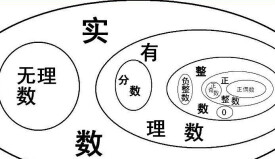
實數,是有理數和無理數的總稱。數學上,實數定義為與數軸上的點相對應的數。實數可以直觀地看作有限小數與無限小數,實數和數軸上的點一一對應。但僅僅以列舉的方式不能描述實數的整體。實數和虛數共同構成複數。
實數可以分為有理數和無理數兩類,或代數數和超越數兩類。實數集通常用黑正體字母 R 表示。R表示n維實數空間。實數是不可數的。實數是實數理論的核心研究對象。
所有實數的集合則可稱為實數系(real number system)或實數連續統。任何一個完備的阿基米德有序域均可稱為實數系。在保序同構意義下它是惟一的,常用R表示。由於R是定義了算數運算的運算系統,故有實數系這個名稱。
實數可以用來測量連續的量。理論上,任何實數都可以用無限小數的方式表示,小數點的右邊是一個無窮的數列(可以是循環的,也可以是非循環的)。在實際運用中,實數經常被近似成一個有限小數(保留小數點后 n 位,n為正整數)。在計算機領域,由於計算機只能存儲有限的小數位數,實數經常用浮點數來表示。
實數可實現的基本運算有加、減、乘、除、乘方等,對非負數(即正數和0)還可以進行開方運算。實數加、減、乘、除(除數不為零)、平方后結果還是實數。任何實數都可以開奇次方,結果仍是實數,只有非負實數,才能開偶次方其結果還是實數。
實數集對加、減、乘、除(除數不為零)四則運算具有封閉性,即任意兩個實數的和、差、積、商(除數不為零)仍然是實數。
實數集是有序的,即任意兩個實數a、b必定滿足並且只滿足下列三個關係之一:,,。
實數大小具有傳遞性,即若,且,則有。
實數具有阿基米德性質(Archimedean property),即,,,則∃正整數n,。
實數集具有稠密性,即兩個不相等的實數之間必有另一個實數,既有有理數,也有無理數.
作為度量空間或一致空間,實數集合是個完備空間,它有以下性質:
一. 所有實數的柯西序列都有一個實數極限。
有理數集合就不是完備空間。例如,(1, 1.4, 1.41, 1.414, 1.4142, 1.41421, ...) 是有理數的柯西序列,但沒有有理數極限。實際上,它有個實數極限。
實數是有理數的完備化——這亦是構造實數集合的一種方法。
極限的存在是微積分的基礎。實數的完備性等價於歐幾里德幾何的直線沒有“空隙”。
二. “完備的有序域”
實數集合通常被描述為“完備的有序域”,這可以幾種解釋。
首先,有序域可以是完備格。然而,很容易發現沒有有序域會是完備格。這是由於有序域沒有最大元素(對任意元素z,將更大)。所以,這裡的“完備”不是完備格的意思。
另外,有序域滿足戴德金完備性,這在上述公理中已經定義。上述的唯一性也說明了這裡的“完備”是指戴德金完備性的意思。這個完備性的意思非常接近採用戴德金分割來構造實數的方法,即從(有理數)有序域出發,通過標準的方法建立戴德金完備性。
R這兩個完備性的概念都忽略了域的結構。然而,有序群(域是種特殊的群)可以定義一致空間,而一致空間又有完備空間的概念。上述完備性中所述的只是一個特例。(這裡採用一致空間中的完備性概念,而不是相關的人們熟知的度量空間的完備性,這是由於度量空間的定義依賴於實數的性質。)當然,並不是唯一的一致完備的有序域,但它是唯一的一致完備的阿基米德域。實際上,“完備的阿基米德域”比“完備的有序域”更常見。可以證明,任意一致完備的阿基米德域必然是戴德金完備的(當然反之亦然)。這個完備性的意思非常接近採用柯西序列來構造實數的方法,即從(有理數)阿基米德域出發,通過標準的方法建立一致完備性。
“完備的阿基米德域”最早是由希爾伯特提出來的,他還想表達一些不同於上述的意思。他認為,實數構成了最大的阿基米德域,即所有其他的阿基米德域都是R的子域。這樣R是“完備的”是指,在其中加入任何元素都將使它不再是阿基米德域。這個完備性的意思非常接近用超實數來構造實數的方法,即從某個包含所有(超實數)有序域的純類出發,從其子域中找出最大的阿基米德域。
R如果在一條直線(通常為水平直線)上確定O作為原點,指定一個方向為正方向(通常把指向右的方向規定為正方向),並規定一個單位長度,則稱此直線為數軸。任一實數都對應與數軸上的唯一一個點;反之,數軸上的每一個點也都唯一的表示一個實數。於是,實數集與數軸上的點有著一一對應的關係。
實數集是不可數的,也就是說,實數的個數嚴格多於自然數的個數(儘管兩者都是無窮大)。這一點,可以通過康托爾對角線方法證明。實際上,實數集的勢為(請參見連續統的勢),即自然數集的冪集的勢。由於實數集中只有可數集個數的元素可能是代數數,絕大多數實數是超越數。實數集的子集中,不存在其勢嚴格大於自然數集的勢且嚴格小於實數集的勢的集合,這就是連續統假設。事實上這假設獨立於ZFC集合論,在ZFC集合論內既不能證明它,也不能推出其否定。
所有非負實數的平方根屬於R,但這對負數不成立。這表明R上的序是由其代數結構確定的。而且,所有奇數次多項式至少有一個根屬於R。這兩個性質使成為實封閉域的最主要的實例。證明這一點就是對代數基本定理的證明的前半部分。
實數集擁有一個規範的測度,即勒貝格測度。
實數集的上確界公理用到了實數集的子集,這是一種二階邏輯的陳述。不可能只採用一階邏輯來刻畫實數集:1. Löwenheim–Skolem theorem定理說明,存在一個實數集的可數稠密子集,它在一階邏輯中正好滿足和實數集自身完全相同的命題;2. 超實數的集合遠遠大於R,但也同樣滿足和R一樣的一階邏輯命題。滿足和R一樣的一階邏輯命題的有序域稱為R的非標準模型。這就是非標準分析的研究內容,在非標準模型中證明一階邏輯命題(可能比在中證明要簡單一些),從而確定這些命題在R中也成立。
實數集構成一個度量空間:x和y間的距離定為絕對值。作為一個全序集,它也具有序拓撲。這裡,從度量和序關係得到的拓撲相同。實數集又是 1 維的可縮空間(所以也是連通空間)、局部緊緻空間、可分空間、貝利空間。但實數集不是緊緻空間。這些可以通過特定的性質來確定,例如,無限連續可分的序拓撲必須和實數集同胚。以下是實數的拓撲性質總覽:
i.令a為一實數。a的鄰域是實數集中一個包括一段含有a的線段的子集。
ii.R是可分空間。
iii.Q在R中處處稠密。
iv.R的開集是開區間的聯集。
v.R的緊子集是有界閉集。特別是:所有含端點的有限線段都是緊子集。
vi.每個R中的有界序列都有收斂子序列。
vii.R是連通且單連通的。
viii.R中的連通子集是線段、射線與R本身。由此性質可迅速導出中間值定理。
從有理數構造實數
實數可以用通過收斂於一個唯一實數的十進位或二進位展開。如所定義的序列的方式而構造為有理數的補全。實數可以不同方式從有理數構造出來。這裡給出公理的方法。
設R是所有實數的集合,則:Ⅰ集合R是一個域:可以作加、減、乘、除運算,且有如交換律,結合律等常見性質。
Ⅱ域R是個有序域,即存在全序關係≥R,對所有實數x,y和z;
Ⅲ若則;
Ⅳ若且則。
Ⅴ集合R滿足完備性,即任意R的有非空子集S,即, ,若S在R內有上界,那麼S在R內有上確界。
最後一條是區分實數和有理數的關鍵。例如對於所有平方小於2的有理數的集合,它在有理數集內有上界,例如1.5;但在有理數集內無上確界(因為不是有理數)。
實數通過上述性質唯一確定。更準確的說,給定任意兩個有序域和,存在從到的唯一的域同構,即結構上兩者可看作是相同的。
整數和小數的集合也是實數,實數的定義是:有理數和無理數的集合。而整數和分數統稱有理數,小數分為有限小數,無限循環小數,無限不循環小數(即無理數),其中有限小數和無限循環小數均能化為分數,所以小數即為分數和無理數的集合,加上整數,即為整數-分數-無理數,也就是有理數-無理數,即實數。
在公元前500年左右,以畢達哥拉斯為首的希臘數學家們認識到有理數在幾何上不能滿足需要,但畢達哥拉斯本身並不承認無理數的存在。直到17世紀,實數才在歐洲被廣泛接受。18世紀,微積分學在實數的基礎上發展起來。1871年,德國數學家康托爾第一次提出了實數的嚴格定義。
根據日常經驗,有理數集在數軸上似乎是“稠密”的,於是古人一直認為用有理數即能滿足測量上的實際需要。以邊長為1厘米的正方形為例,其對角線有多長?在規定的精度下(比如誤差小於0.001厘米),總可以用有理數來表示足夠精確的測量結果(比如1.414厘米)。但是,古希臘畢達哥拉斯學派的數學家發現,只使用有理數無法完全精確地表示這條對角線的長度,這徹底地打擊了他們的數學理念;他們原以為:
任何兩條線段(的長度)的比,可以用自然數的比來表示。
正因如此,畢達哥拉斯本人甚至有“萬物皆數”的信念,這裡的數是指自然數(1 , 2 , 3 ,...),而由自然數的比就得到所有正有理數,而有理數集存在“縫隙”這一事實,對當時很多數學家來說可謂極大的打擊(見第一次數學危機)。
從古希臘一直到17世紀,數學家們才慢慢接受無理數的存在,並把它和有理數平等地看作數;後來有虛數概念的引入,為加以區別而稱作“實數”,意即“實在的數”。在當時,儘管虛數已經出現並廣為使用,實數的嚴格定義卻仍然是個難題,以至函數、極限和收斂性的概念都被定義清楚之後,才由十九世紀末的戴德金、康托等人對實數進行了嚴格處理。