二進位
數學和數字電路中指以2為基數的記數系統
二進位(binary)在數學和數字電路中指以2為基數的記數系統,以2為基數代表系統是二進位制的。這一系統中,通常用兩個不同的符號0(代表零)和1(代表一)來表示。數字電子電路中,邏輯門的實現直接應用了二進位,因此現代的計算機和依賴計算機的設備里都用到二進位。每個數字稱為一個比特(Bit,Binary digit的縮寫)
二進位數據的表示法:
【例1102】將二進位數據111.01寫成加權係數的形式。
解:
二進位和十六進位,八進位一樣,都以二的冪來進位的。
有四種情況: 0+0=0
0+1=1
1+0=1
1+1=10
0 進位為1
【例1103】求 1011(2)+11(2)的和
解:
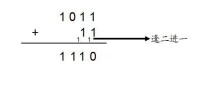
1011+11
有四種情況: 0×0=0
1×0=0
0×1=0
1×1=1
0-0=0,1-0=1,1-1=0,0-1=1。
0÷1=0,1÷1=1。
拈加法二進位是加減乘除外的一種特殊演演算法。
拈加法運算與進行加法類似,但不需要做進位。此演演算法在博弈論(Game Theory)中被廣泛利用
計算機中的十進位小數轉換二進位
計算機中的十進位小數用二進位通常是用乘二取整法來獲得的。
比如0.65換算成二進位就是:
0.65 × 2 = 1.3 取1,留下0.3繼續乘二取整

二進位
0.6 × 2 = 1.2 取1,留下0.2繼續乘二取整
0.2 × 2 = 0.4 取0,留下0.4繼續乘二取整
0.4 × 2 = 0.8 取0,留下0.8繼續乘二取整
0.8 × 2 = 1.6 取1,留下0.6繼續乘二取整
0.6 × 2 = 1.2 取1,留下0.2繼續乘二取整
.......
一直循環,直到達到精度限制才停止(所以,計算機保存的小數一般會有誤差,所以在編程中,要想比較兩個小數是否相等,只能比較某個精度範圍內是否相等)。這時,十進位的0.65,用二進位就可以表示為:0.1010011。
還值得一提的是,在計算機中,除了十進位是有符號的外,其它如二進位、八進位、16進位都是無符號的。
在現實生活和記數器中,如果表示數的“器件”只有兩種狀態,如電燈的“亮”與“滅”,開關的“開”與“關”。一種狀態表示數碼0,另一種狀態表示數碼1,1加1應該等於2,因為沒有數碼2,只能向上一個數位進一,就是採用“滿二進一”的原則,這和十進位是採用“滿十進一”原則完全相同。
1+1=10,10+1=11,11+1=100,100+1=101,
101+1=110,110+1=111,111+1=1000,……,
可見二進位的10表示二,100表示四,1000表示八,10000表示十六,……。
二進位同樣是“位值制”。同一個數碼1,在不同數位上表示的數值是不同的。如11111,從右往左數,第一位的1就是一,第二位的1表示二,第三位的1表示四,第四位的1表示八,第五位的1表示十六。
所謂二進位,也就是計算機運算時用的一種演演算法。二進位只由一和零組成。
比方說吧,你上一年級時一定聽說過“進位筒”(“數位筒”)吧!十進位是個位上滿十根小棒就捆成一捆,放進十位筒,十位筒滿十捆就捆成一大捆,放進百位筒……
二進位也是一樣的道理,個位筒上滿2根就向十位進一,十位上滿兩根就向百位進一,百位上滿兩根…… 二進位是世界上第一台計算機上用的演演算法,最古老的計算機里有一個個燈泡,當運算的時候,比如要表達“一”,第一個燈泡會亮起來。要表達“二”,則第一個燈泡熄滅,第二個燈泡就會亮起來。
二進位就是等於2時就要進位。
0=00000000
1=00000001
2=00000010
3=00000011
4=00000100
5=00000101
6=00000110
7=00000111
8=00001000
9=00001001
10=00001010
……
即是逢二進一,二進位廣泛用於最基礎的運算方式,計算機的運行計算基礎就是基於二進位來運行。只是用二進位執行運算,用其他進位表現出來。
其實把二進位三位一組分開就是八進位, 四位一組就是十六進位

二進位
二進位數、八進位數、十六進位數轉換為十進位數的方法:按權展開求和法
(1)二進位轉十進位
方法:“按權展開求和”
【例】:
規律:個位上的數字的次數是0,十位上的數字的次數是1,......,依次遞增,而十分位的數字的次數是-1,百分位上數字的次數是-2,......,依次遞減。
注意:不是任何一個十進位小數都能轉換成有限位的二進位數。
(2)十進位轉二進位
· 十進位整數轉二進位數:“除以2取余,逆序排列”(除二取余法)
【例】:
89÷2 ……1
44÷2 ……0
22÷2 ……0
11÷2 ……1
5÷2 ……1
2÷2 ……0
1
· 十進位小數轉二進位數:“乘以2取整,順序排列”(乘2取整法)
【例】: (0.625)10= (0.101)2
0.625X2=1.25 ……1
0.25 X2=0.50 ……0
0.50 X2=1.00 ……1
十進位1至128的二進位表示:
0=0
1=1
2=10
3=11
4=100
5=101
6=110
7=111
8=1000
9=1001
10=1010
11=1011
12=1100
13=1101
14=1110
15=1111
16=10000
17=10001
18=10010
19=10011
20=10100
21=10101
22=10110
23=10111
24=11000
25=11001
26=11010
27=11011
28=11100
29=11101
30=11110
31=11111
32=100000
33=100001
34=100010
35=100011
36=100100
37=100101
38=100110
39=100111
40=101000
41=101001
42=101010
43=101011
44=101100
45=101101
46=101110
47=101111
48=110000
49=110001
50=110010
51=110011
52=110100
53=110101
54=110110
55=110111
56=111000
57=111001
58=111010
59=111011
60=111100
61=111101
62=111110
63=111111
64=1000000
65=1000001
66=1000010
67=1000011
68=1000100
69=1000101
70=1000110
71=1000111
72=1001000
73=1001001
74=1001010
75=1001011
76=1001100
77=1001101
78=1001110
79=1001111
80=1010000
81=1010001
82=1010010
83=1010011
84=1010100
85=1010101
86=1010110
87=1010111
88=1011000
89=1011001
90=1011010
91=1011011
92=1011100
93=1011101
94=1011110
95=1011111
96=1100000
97=1100001
98=1100010
99=1100011
100=1100100
101=1100101
102=1100110
103=1100111
104=1101000
105=1101001
106=1101010
107=1101011
108=1101100
109=1101101
110=1101110
111=1101111
112=1110000
113=1110001
114=1110010
115=1110011
116=1110100
117=1110101
118=1110110
119=1110111
120=1111000
121=1111001
122=1111010
123=1111011
124=1111100
125=1111101
126=1111110
127=1111111
128=10000000
.十進位負數轉二進位:“先取正數的二進位值,再取反,加1”
【例】:(-31) = (1)
31的二進位數為11111,取反00000,加1得1。
二進位數轉換成八進位數:從小數點開始,整數部分向左、小數部分向右,每3位為一組用一位八進位數的數字錶示,不足3位的要用“0”補足3位,就得到一個八進位數。
八進位數轉換成二進位數:把每一個八進位數轉換成3位的二進位數,就得到一個二進位數。
八進位數字與十進位數字對應關係如下:
000 -> 0 | 004-> 4 | 010=8
001 -> 1 |005 -> 5| 011=9
002 -> 2 |006 -> 6 | 012=10
003 -> 3 |007 -> 7 | 013=11
【例】:將八進位的37.416轉換成二進位數:
3 7 . 4 1 6
011 111 .100 001 110
即:(37.416)8 =(11111.10000111)2
【例】:將二進位的10110.0011 轉換成八進位:
0 1 0 1 1 0 . 0 0 1 1 0 0
2 6 . 1 4
即:(10110.0011)2 = (26.14)8
二進位數轉換成十六進位數:二進位數轉換成十六進位數時,只要從小數點位置開始,向左或向右每四位二進位劃分一組(不足四位數可補0),然後寫出每一組二進位數所對應的十六進位數碼即可。
十六進位數轉換成二進位數:把每一個十六進位數轉換成4位的二進位數,就得到一個二進位數。
十六進位數字與二進位數字的對應關係如下:
0000 -> 0 0100 -> 4 1000 -> 8 1100 -> C
0001 -> 1 0101 -> 5 1001 -> 9 1101 -> D
0010 -> 2 0110 -> 6 1010 -> A 1110 -> E
0011 -> 3 0111 -> 7 1011 -> B 1111 -> F
【例】:將十六進位數5DF.9 轉換成二進位:
5 D F . 9
0101 1101 1111 .1001
即:(5DF.9)16 =(10111011111.1001)2{十六進位怎麼會有小數點}
【例】:將二進位數1100001.111 轉換成十六進位:
0110 0001 . 1110
6 1 . E
即:(1100001.111)2 =(61.E)16
與十進位的區別
二進位與十進位的區別在於數碼的個數和進位規律有很大的區別,顧名思義,二進位的計數規律為逢二進一,是以2為基數的計數體制。10這個數在二進位和十進位中所表示的意義完全不同,在十進位中就是我們通常所說的十,在二進位中,其中的一個意義可能是表示一個大小等價於十進位數2的數值。

十進位與二進位的關係
一般地,任意二進位數可表示為:
例題 1.3.2 試將二進位數(01010110)B轉換為十進位數。
解:將每一位二進位數乘以位權后相加便得相應的十進位數
在數字電子技術和計算機應用中,二值數據常用數字波形來表示
。使用數字波形可以使得數據比較直觀,也便於使用電子示波器進行監視。圖1.3.3表示一計數器的波形。
圖1.3.3 用二進位數表示0~15波形圖
圖中給出了四個二進位波形。看這種二進位波形圖時,我們應當沿著圖中虛線所示的方向來看,即使圖中沒有標出虛線(一般都沒有標出),也要想象出虛線來。其中在每一個波形上方的數字錶示了與波形對應的位的數值,最後一行則是相應的十進位數,其中LSB是英文Least Significant Bit的縮寫,表示最低位,MSB是Most Significant Bit的縮寫,表示二進位數的最高位。顯然,這是一組4位的二進位數,總共有16組,最左邊的二進位數為0000,最上邊的波形代表二進位數的最低位,也就是通常在十進位數中我們所說的個位數,最下面的是最高位。圖中最右邊的二進位數為1111,對應的十進位數為15。再來看看對應於十進位數5的二進位數是多少呢?是0101,對了,讀數的順序是從下往上。
二進位數在數字系統(比如計算機之間)中的傳輸的方式分為串列和并行兩種。
其中串列傳輸時二進位數是按照逐位傳遞的方式進行傳輸,根據實際情況可以從最高位或最低位開始傳輸,一般情況下是從最高位開始傳輸的。只需要一根數據線。如圖1.3.4所示,要完成八位二進位數的傳輸,需要經歷八個時鐘周期。
圖1.3.4 二進位數據的串列傳輸
(a) 兩台計算機之間的串列通信 (b) 二進位數據的串列表示
典型的例子是數據機與計算機之間的通信就是通過串列傳輸來完成的。
并行傳輸的效率要高於串列傳輸,一次可以傳輸完整的一組二進位數。但是根據所要傳輸的二進位數的位數的多少,需要備足足夠多的數據線。一般來說,常見的并行傳輸採用的數據線有8、16、32等,再多就很少見了。典型的并行傳輸例子是印表機與計算機之間的通信傳輸,見圖1.3.5。
圖1.3.5 并行傳輸數據的示意圖
(a) 計算機與印表機之間的并行通信 (b) 二進位數據的并行表示
圖1.3.5顯示了採用并行傳輸模式,只需要一個時鐘周期,即可完成八位二進位數的傳輸。
不同進位之間的轉換本質就是確定各個不同權值位置上的數碼。轉換正整數的進位的有一個簡單演演算法,就是通過用目標基數作長除法;餘數給出從最低位開始的“數字” 。例如,1020304從10進位轉到7進位:
用ftp工具以二進位方式上傳
萊布尼茨不僅發明了二進位,而且賦予了它宗教的內涵。他在寫給當時在中國傳教的法國耶穌士會牧師布維(Joachim Bouvet,1662 - 1732)的信中說:“第一天的伊始是1,也就是上帝。第二天的伊始是2,……到了第七天,一切都有了。所以,這最後的一天也是最完美的。因為,此時世間的一切都已經被創造出來了。因此它被寫作‘7’,也就是‘111’(二進位中的111等於十進位的7),而且不包含0。只有當我們僅僅用0和1來表達這個數字時,才能理解,為什麼第七天才最完美,為什麼7是神聖的數字。特別值得注意的是它(第七天)的特徵(寫作二進位的111)與三位一體的關聯。”
布維是一位漢學大師,他對中國的介紹是17、18世紀歐洲學界中國熱最重要的原因之一。布維是萊布尼茨的好朋友,一直與他保持著頻繁的書信往來。萊布尼茨曾將很多布維的文章翻譯成德文,發表刊行。恰恰是布維向萊布尼茨介紹了《周易》和八卦的系統,並說明了《周易》在中國文化中的權威地位。
八卦是由八個符號組構成的占卜系統,而這些符號分為連續的與間斷的橫線兩種。這兩個後來被稱為“陰”、“陽”的符號,在萊布尼茨眼中,就是他的二進位的中國翻版,但實際萊布尼茨是受中國陰陽太極影響,只不過他付出了諸多研究,推演出二進位。他感到這個來自古老中國文化的符號系統與他的二進位之間的關係實在太明顯了,因此斷言:二進位乃是具有世界普遍性的、最完美的邏輯語言。
另一個可能引起萊布尼茨對八卦的興趣的人是坦澤爾(Wilhelm Ernst Tentzel),他當時是圖靈根大公爵硬幣珍藏室的領導,也是萊布尼茨的好友之一。在他主管的這個硬幣珍藏中有一枚印有八卦符號的硬幣。
與中國易經聯繫

二進位
白晉很驚訝,因為他發現這種“二進位的算術”與中國古代的一種建立在兩個符號基礎上的符號系統是非常近似的,這兩個符號分別由一條直線和兩條短線組成,即── 和 — —。這是中國最著名大概也是最古老的書《易經》的基本組成部分,據今人推測,該書大約產生於公元前第一個千年的初期,開始主要是一部占卜用書,裡邊的兩個符號可能分別代表“是”和“不”。萊布尼茨對這個相似也很吃驚,和他的筆友白晉一樣,他也深信《易經》在數學上的意義。他相信古代的中國人已經掌握了二進位並在科學方面遠遠超過當代的中國人。
這一次將數學與古代中國《易經》相聯的嘗試是不符合實際的。萊布尼茨的二進位數學指向的不是古代中國,而是未來。萊布尼茨在1679年3月15日記錄下他的二進位體系的同時,還設計了一台可以完成數碼計算的機器。我們今天的現代科技將此設想變為現實,這在萊布尼茨的時代是超乎人的想象能力的。
數字裝置簡單可靠,所用元件少;
只有兩個數碼0和1,因此它的每一位數都可用任何具有兩個不同穩定狀態的元件來表示;
基本運算規則簡單,運算操作方便。
用二進位表示一個數時,位數多。因此實際使用中多採用送入數字系統前用十進位,送入機器后再轉換成二進位數,讓數字系統進行運算,運算結束后再將二進位轉換為十進位供人們閱讀。
二進位和十六進位的互相轉換比較重要。不過這二者的轉換卻不用計算,每個C,C++程序員都能做到看見二進位數,直接就能轉換為十六進位數,反之亦然。
我們也一樣,只要學完這一小節,就能做到。
首先我們來看一個二進位數:1111,它是多少呢?
你可能還要這樣計算:1 × 2º + 1 × 2¹ + 1 × 2² + 1 × 2³ = 1 × 1 + 1 × 2 + 1 × 4 + 1 × 8 = 15。
然而,由於1111才4位,所以我們必須直接記住它每一位的權值,並且是從高位往低位記,:8、4、2、1。即,最高位的權值為2³ = 8,然後依次是 2² = 4,2¹=2, 2º = 1。
記住8421,對於任意一個4位的二進位數,我們都可以很快算出它對應的10進位值。
下面列出四位二進位數 xxxx 所有可能的值(中間略過部分)
僅4位的2進位數快速計算方法 十進位值 十六進值
1111 = 8 + 4 + 2 + 1 = 15 F
1110 = 8 + 4 + 2 + 0 = 14 E
1101 = 8 + 4 + 0 + 1 = 13 D
1100 = 8 + 4 + 0 + 0 = 12 C
1011 = 8 + 0 + 2+ 1 = 11 B
1010 = 8 + 0 + 2 + 0 = 10 A
1001 = 8 + 0 + 0 + 1 = 9
....
0001 = 0 + 0 + 0 + 1 = 1
0000 = 0 + 0 + 0 + 0 = 0 0
二進位數要轉換為十六進位,就是以4位一段,分別轉換為十六進位。
如(上行為二制數,下面為對應的十六進位):
1111 1101 , 1010 0101 , 1001 1011
F D , A 5 , 9 B
反過來,當我們看到 FD時,如何迅速將它轉換為二進位數呢?
先轉換F:
看到F,我們需知道它是15(可能你還不熟悉A~F這六個數),然後15如何用8421湊呢?應該是8 + 4 + 2 + 1,所以四位全為1 :1111。
接著轉換 D:
看到D,知道它是13,13如何用8421湊呢?應該是:8 + 4 + 1,即:1101。
所以,FD轉換為二進位數,為: 1111 1101
由於十六進位轉換成二進位相當直接,所以,我們需要將一個十進位數轉換成2進位數時,也可以先轉換成16進位,然後再轉換成2進位。
比如,十進位數 1234轉換成二制數,如果要一直除以2,直接得到2進位數,需要計算較多次數。所以我們可以先除以16,得到16進位數:
被除數 計算過程 商 餘數
1234 1234/16 77 2
77 77/16 4 13 (D)
4 4/16 0 4
結果16進位為: 0x4D2
同樣,如果一個二進位數很長,我們需要將它轉換成10進位數時,除了前面學過的方法是,我們還可以先將這個二進位轉換成16進位,然後再轉換為10進位。
首先,二進位計數制僅用兩個數碼。0和1,所以,任何具有二個不同穩定狀態的元件都可用來表示數的某一位。而在實際上具有兩種明顯穩定狀態的元件很多。例如,氖燈的"亮"和"熄";開關的”開“和”關“; 電壓的”高“和”低“、”正“和”負“;紙帶上的”有孔“和“無孔”,電路中的”有信號“和”無信號“, 磁性材料的南極和北極等等,不勝枚舉。利用這些截然不同的狀態來代表數字,是很容易實現的。不僅如此,更重要的是兩種截然不同的狀態不單有量上的差別,而且是有質上的不同。這樣就能大大提高機器的抗干擾能力,提高可靠性。而要找出一個能表示多於二種狀態而且簡單可靠的器件,就困難得多了。
其次,二進位計數制的四則運算規則十分簡單。而且四則運算最後都可歸結為加法運算和移位,這樣,電子計算機中的運算器線路也變得十分簡單了。不僅如此,線路簡化了,速度也就可以提高。這也是十進位計數制所不能相比的。
第三,在電子計算機中採用二進位表示數可以節省設備。可 以從理論上證明,用三進位制最省設備,其次就是二進位制。但由於二進位制有包括三進位制在內的其他進位制所沒有的優點,所以大多數電子計算機還是採用二進位。此外,由於二進位中只用二個符號“ 0”和“1”,因而可用布爾代數來分析和綜合機器中的邏輯線路。這為設計電子計算機線路提供了一個很有用的工具。
第四,二進位的符號“1”和“0”恰好與邏輯運算中的“對”(true)與“錯”(false)對應,便於計算機進行邏輯運算。
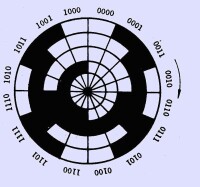
二進位循環編碼盤
我們平時來取數據是這樣用的!
Getdata=rs("fieldname")
而取二進位就得這樣
size=rs("fieldname").acturalsize
getdata=rs("fieldname").getchunk(size)
我們從上面看到,我們取二進位數據必須先得到它的大小,然後再搞定它,這個好像是ASP中處理二進位數據的常用方法,我們在獲取從客戶端傳來的所有數據時,也是用的這種方法。
下面我們也來看看是怎樣將二進位數據加入資料庫
rs("fieldname").appendchunk binarydata
一步搞定!
另外,使用getchunk和appendchunk將數據一步一步的取出來!
下面演示一個取數據的例子!
Addsize=2
totalsize=rs("fieldname").acturalsize
offsize=0
Do Where offsize Binarydata=rs("fieldname").getchunk(offsize)
data=data&Binarydata
offsize=offsize+addsize
Loop
當這個程序運行完畢時,data就是我們取出的數據.
從小數點開始3位(不足3位補0)二進位數得到1位八進位數
(用B代表二進位,用O代表八進位):000B=0O、001B=1O、010B=2O、011B=3O、100B=4O、101B=5O、110B=6O。
二進位與十進位的“1248"換演演算法:例
| 十進位 | 16 | 8 | 4 | 2 | 1 |
| 二進位 | 1 | 1 | 1 |
即16+4+1=21
簡單來說,就是把二進位數代入表格內,十進位數不變,只要把有十進位中對應1的數加起來就可以得出結果。
進位
在基數b的位置記數系統(其中b是一個正自然數,叫做基數),b個基本符號(或者叫數字)對應於包括0的最小b個自然數。要產生其他的數,符號在數中的位置要被用到。最後一位的符號用它本身的值,向左一位其值乘以b。一般來講,若b是基底,我們在b進位系統中的數表示為 的形式,並按次序寫下數字a0a1a2a3...ak。這些數字是0到b-1的自然數。
一般來講,b進位系統中的數有如下形式:
數 和 是相應數字的比重。
二進位計數
17世紀至18世紀的德國數學家萊布尼茨,是世界上第一個提出二進位記數法的人。用二進位記數,只用0和1兩個符號,無需其他符號。
二進位數據也是採用位置計數法,其位權是以2為底的冪。例如二進位數據110.11,逢2進1,其權的大小順序為2²、2¹、2º、 、 。對於有n位整數,m位小數的二進位數據用加權係數展開式表示,可寫為:
二進位數據一般可寫為:
【例】:將二進位數據111.01寫成加權係數的形式。
解:
二進位和十六進位,八進位一樣,都以二的冪來進位的。
