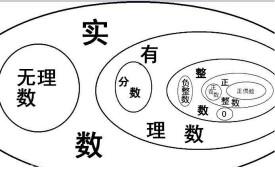
實數理論

實數是數學中最基本的概念之一。實數與數軸上的點可以一一對應。數學分析所研究的函數，其自變數都取實數值，因此認識和了解實數是建立嚴格的分析理論不可缺少的基礎（“分析基礎”）。實數包括有理數與無理數，而從歐幾里得以來，人們都把它們理解為單位長線段可公度與不可公度的線段的長度。到17世紀，人們對實數的使用已經習以為常，並開始脫離其幾何原型抽象地認識實數。但到19世紀中葉，在分析嚴格化的進程中，由於一些事實無法證明（例如，柯西無法證明自己提出的收斂準則的充分性），一些證明出了錯（如波爾查諾對連續函數介值性的證明），人們才發現對實數特別是無理數的認識仍然模糊不清，這才促使一批數學家關注於處理無理數的問題。通過他們的努力，終於在將近半個世紀的時間裡，建立了多種形式上不同，而實質上等價的嚴格的實數理論。各種形式的構造性實數理論，都是首先從有理數出發去定義無理數，也就是說，數軸上有理點之間的所有空隙（無理點），都可以由有理數經過一定的方式來確定。然後證明這樣定義的實數（原有的有理數和新定義的無理數）具有人們原來熟知的實數所應有的一切性質，特別是連續性。這些形式上不同的實數理論也就因確定空隙的方法不同而互相區分，它們主要有：戴德金用有理數的分割的方法，康托爾用有理數的基本列的方法，魏爾斯特拉斯用無窮（非循環）十進小數的方法，以及用端點為有理點的閉區間套和有界單調有理數列的方法。站在現代數學的立場來看，上述各種方法都是從假定實數具有某種特性出發的（如戴德金的方法假定了實數的連續性，康托爾假定的是完備性，而用閉區間套的方法反映了實軸上有界閉集的緊性），而這些特性在實數範圍內都是等價的，因而用這些方法定義出的實數都是完全相同的。此外，還有一種與上述構造法完全不同的定義實數的方法（即“實數公理”）。他將實數應有的一些基本性質列為一個公理系統，然後將滿足這個公理系統的對象定義為實數。基於這些公理的實數理論與上述基於構造法的也相互等價。

當然還應當指出，不僅極限理論需要在實數系中才能成立，就是中學數學中的許多初等函數，除了多項式和有理分式之外，沒有實數也是無法給出定義的。將無限不循環小數定義為無理數是容易為學生所接受的，但在這樣定義的實數系內四則運算是如何進行的，還是完全不清楚的，而且實際上也不是簡單的。至於指數和對數 當其中都是實數時應當如何定義就更加困難了。由此可見，即使為了對初等函數給出嚴格的定義，也需要回答什麼是實數這樣一個問題。當然這不是中學數學要承擔的任務。

公元前500年，古希臘畢達哥拉斯(Pythagoras)學派的弟子希帕索斯(Hippasus)發現了一個驚人的事實，一個正方形的對角線與其一邊的長度是不可公度的(若正方形邊長是1，則對角線的長不是一個有理數)這一不可公度性與畢氏學派“萬物皆為數”(指有理數)的哲理大相徑庭。這一發現使該學派領導人惶恐、惱怒，認為這將動搖他們在學術界的統治地位。希帕索斯因此被囚禁，受到百般折磨，最後竟遭到沉舟身亡的懲處。

畢氏弟子的發現，第一次向人們揭示了有理數系的缺陷，證明它不能同連續的無限直線同等看待，有理數並沒有布滿數軸上的點，在數軸上存在著不能用有理數表示的“孔隙”。而這種“孔隙”經後人證明簡直多得“不可勝數”。於是，古希臘人把有理數視為連續銜接的那種算術連續統的設想徹底地破滅了。不可公度量的發現連同著名的芝諾悖論一同被稱為數學史上的第一次危機（第一次數學危機），對以後2000多年數學的發展產生了深遠的影響，促使人們從依靠直覺、經驗而轉向依靠證明，推動了公理幾何學與邏輯學的發展，並且孕育了微積分的思想萌芽。

不可通約的本質是什麼？長期以來眾說紛壇，得不到正確的解釋，兩個不可通約的比值也一直被認為是不可理喻的數。15世紀義大利著名畫家達。芬奇稱之為“無理的數”，17世紀德國天文學家開普勒稱之為“不可名狀”的數。

然而，真理畢竟是淹沒不了的，畢氏學派抹殺真理才是“無理”。人們為了紀念希帕索斯這位為真理而獻身的可敬學者，就把不可通約的量取名為“無理數”——這便是“無理數”的由來。

無理數的發現，擊碎了畢達哥拉斯學派“萬物皆數”的美夢。同時暴露出有理數系的缺陷：一條直線上的有理數儘管是“稠密”，但是它卻漏出了許多“孔隙”，而且這種“孔隙”多的“不可勝數”。這樣，古希臘人把有理數視為是連續銜接的那種算術連續統的設想，就徹底的破滅了。它的破滅，在以後兩千多年時間內，對數學的發展，起到了深遠的影響。不可通約的本質是什麼？長期以來眾說紛紜。兩個不可通約量的比值也因其得不到正確的解釋，而被認為是不可理喻的數。15世紀達芬奇（LeonardodaVinci,1452-1519）把它們稱為是“無理的數”（irrationalnumber），開普勒（J.Kepler,1571-1630）稱它們是“不可名狀”的數。這些“無理”而又“不可名狀”的數，找到雖然在後來的運算中漸漸被使用，但是它們究竟是不是實實在在的數，卻一直是個困擾人的問題。

中國古代數學在處理開方問題時，也不可避免地碰到無理根數。對於這種“開之不盡”的數，《九章算術》直截了當地“以面命之”予以接受，劉徽註釋中的“求其微數”，實際上是用10進小數來無限逼近無理數。這本是一條完成實數系統的正確道路，只是劉徽的思想遠遠超越了他的時代，而未能引起後人的重視。不過，中國傳統數學關注的是數量的計算，對數的本質並沒有太大的興趣，而善於究根問底的希臘人就無法邁過這道坎了。既然不能克服它，那就只好迴避它。此後的希臘數學家，如歐多克斯（Eudoxus）、歐幾里得（Euclid）在他們的幾何學里，都嚴格避免把數與幾何量等同起來。歐多克斯的比例論（見《幾何原本》第5卷），使幾何學在邏輯上繞過了不可公度的障礙，但就在這以後的漫長時期中，形成了幾何與算術的顯著分離。

17、18世紀微積分的發展幾乎吸引了所有數學家的注意力，恰恰是人們對微積分基礎的關注，使得實數域的連續性問題再次突顯出來。因為，微積分是建立在極限運算基礎上的變數數學，而極限運算，需要一個封閉的數域。無理數正是實數域連續性的關鍵。

無理數是什麼？法國數學家柯西（A.Cauchy,1789-1875）給出了回答：無理數是有理數序列的極限。然而按照柯西的極限定義，所謂有理數序列的極限，意即預先存在一個確定的數，使它與序列中各數的差值，當序列趨於無窮時，可以任意小。但是，這個預先存在的“數”，又從何而來呢？在柯西看來，有理序列的極限，似乎是先驗地存在的。這表明，柯西儘管是那個時代大分析學家，但仍未能擺脫兩千多年來以幾何直覺為立論基礎的傳統觀念的影響。

變數數學獨立建造完備數域的歷史任務，終於在19世紀後半葉，由魏爾斯特拉斯（Weierstrass,1815-1897）、戴德金（R.Dedekind1831-1916）、康托（G.Cantor,1845-1918）等人加以完成了。

1872年，是近代數學史上最值得紀念的一年。這一年，克萊因（F.Kline,1849-1925）提出了著名的“埃爾朗根綱領”（ErlangerProgramm），魏爾斯特拉斯給出了處處連續但處處不可微函數的著名例子。也正是在這一年，實數的三大派理論：戴德金“分割”理論；康托的“基本序列”理論，以及魏爾斯特拉斯的“有界單調序列”理論，同時在德國出現了。

努力建立實數的目的，是為了給出一個形式化的邏輯定義，它既不依賴幾何的含義，又避免用極限來定義無理數的邏輯錯誤。有了這些定義做基礎，微積分中關於極限的基本定理的推導，才不會有理論上的循環。導數和積分從而可以直接在這些定義上建立起來，免去任何與感性認識聯繫的性質。幾何概念是不能給出充分明白和精確的，這在微積分發展的漫長歲月的過程中已經被證明。因此，必要的嚴格性只有通過數的概念，並且在割斷數的概念與幾何量觀念的聯繫之後才能完全達到。這裡，戴德金的工作受到了崇高的評價，這是因為，由“戴德金分割”定義的實數，是完全不依賴於空間與時間直觀的人類智慧的創造物。

實數的三大派理論本質上是對無理數給出嚴格定義，從而建立了完備的實數域。實數域的構造成功，使得兩千多年來存在於算術與幾何之間的鴻溝得以完全填平，無理數不再是“無理的數”了，古希臘人的算術連續統的設想，也終於在嚴格的科學意義下得以實現。

由於實數理論的內容過於龐大，處理方式也各有不同，因此，它的有關理論也散見於各種文獻中，以下是對定義實數系方法的文獻綜述。

所謂公理化方法，起源於古希臘數學家歐幾里得的《幾何原本》。在該書中對於幾何學提出了為數絕少的幾條公理，然後用邏輯推理的方法得到所有其它定理，從而將整個幾何學建成為一個明白易懂又非常嚴格的邏輯體系。只要公理不錯，則所有得到的定理的真理性也就沒有問題。這裡的所謂公理，聽起來似乎抽象，實際上就是大家都能夠接受，對它們的正確性沒有疑問的幾個事實。

所謂實數系的公理化方法也是如此，我們將心目中實數應當具有的儘可能少的獨立性質列出來作為公理，使得其他性質都可以由公理推出來，這就建成了一個公理化系統（“實數公理”）。

希爾伯特公理化方法刻畫了我們所需要的實數系究竟是什麼樣的，它解決了中學數學中有關實數的許多遺留問題，如到底什麼是實數的加法和乘法，為什麼實數的加法滿足交換律、結合律，乘法也滿足交換律、結合律等，可以理解為公理規定的，事實上，如果提供更為基本的假設（比如在有理數的基礎上），這些運算律都是可以證明的。它還保證了實數系的基本定理的成立，為數學分析中極限理論的展開提供了必要的舞台。而滿足這些公理的實數系是否存在，存在性問題是靠下述各種構造方法解決的，也就是給出生成實數系的具體方法，同時證明在其中滿足公理化方法中列出的所有公理。有關公理化的方法可以參看卓里奇的《數學分析（第一卷）》。

實數系的存在性是通過構造法引入的，以下是構造實數系的三種方法（主要是從有理數定義出無理數）。

1.戴德金分割方法

戴德金分割的方法在有關數學分析的著作中多有介紹。最經典的敘述是蘭道特地為此編寫的小書《分析基礎》，這本書的副標題就是“整數、有理數、實數、複數的運算”，該書從自然數出發，一直定義到複數，把完整的數系定義展現了出來。

在前蘇聯的數學分析教材中對戴德金方法做完整敘述的，首推由三卷本組成的經典教材：菲赫金哥爾茨的《微積分學教程》。該書的緒論對戴德金分割方法有完整的敘述，它為全書奠定了牢靠的基礎。另外還可以看亞歷山大羅夫的《集與函數的泛論初階》和辛欽的《數學分析八講》第一講，魯金的《實變函數論》附錄Ⅰ，華東師範大學數學系的《數學分析（第三版）》附錄Ⅱ。

在西方教材中，斯皮瓦克的《微積分》在開始時用兩章詳細介紹了數系的公理，書末又用三章講如何構造實數；盧丁的《數學分析原理》的第一章和附錄有對實數理論簡短的敘述。這兩種教材對戴德金分割的方法都有所改動，從數學史（波耶的《微積分概念史，對導數與積分的歷史性評論》一書中）知道，這基本上就是羅素提出的實數定義方法。

在各種引入實數系的方法中，戴德金分割方法受到了高度的評價，被稱作完全不依賴於空間與時間直觀的人類智慧的創造物。

2.康托爾的基本列（即柯西列）方法

這方面的內容可以參考辛欽的《數學分析簡明教程》第四章，范德瓦爾登的《代數學》第68節，許紹溥、宋國柱等編的《數學分析》第五章，鄒應的《數學分析》第二章以及華東師範大學數學系的《數學分析（第一版）》的附錄Ⅱ。

3.魏爾斯特拉斯從十進小數表示出發的方法

這種方法與前兩個方法不同，不需要引入新的數學對象作為無理數，而是從中學已有的定義出發，即承認十進位有限小數和無限循環小數是有理數，而十進位無限非循環小數則是無理數。這樣就比較容易為中學生所接受。因此也稱為中學生的實數理論。

但為什麼是十進位無限非循環小數？這裡不可避免地涉及到極限問題。在有了柯西準則之後，我們可以從數列極限或無窮級數之和來理解十進位無限非循環小數。但在建立實數系之前是不能如此理解的，否則就與歷史上的柯西犯同樣的錯誤了。

因此，為了避免邏輯上的循環定義，在將十進位無限非循環小數定義為無理數時，一開始不可能將它看成是一個無窮級數的和，而只是將它看成一個純粹的記號，一個還不清楚有什麼意義的數學對象。然後在所有十進位小數全體組成的集合內引入加法、乘法運算，並規定其中任何兩個小數之間的序，並驗證它滿足域公理、序公理、阿基米德公理和連續性公理這4組公理。當然這裡需要經過很多步驟的推論。事實上，認為這樣一種記號代表實數也是一種數學抽象，而且這也是連續性公理的另一種等價形式，歷史上沃利斯於1696年將有理數與循環小數等同。而斯托爾茨則於1886年提出將十進位無限非循環小數作為無理數的定義，但仍未建立起一個滿意的實數理論。

從十進位小數開始講實數的教材很多，例如可以參考阿黑波夫的《數學分析講義》，關肇直的《高等數學教程》和華羅庚的《高等數學引論》等。在張築生的《數學分析新講》的第一章比較詳細的講解了在十進位小數中引入四則運算的嚴格方法。

可以歸入這條途徑的還有一種做法，就是引進以有理數為端點的閉區間套原理作為連續性公理的一種替代物。它既比較直觀，同時又避開了十進位無限非循環小數這類一開始難以說清楚的對象，也是一種好方法。

首先要明白這裡惟一性的確切含義，這裡指的是在同構意義上的惟一性，具體來說，就是證明凡是滿足實數公理的實數系模型都是同構的。

按照戴德金方法建立實數系后對其在同構意義下的惟一性的討論可以參看斯皮瓦克的《微積分》最後一章“實數的惟一性”。按照康托爾的柯西列方法建立實數系時的惟一性的討論可以參看許紹溥、宋國柱等編的《數學分析》第五章的最後部分的證明。