平面圖
測繪學房屋建築學
平面圖(planar graph)是指能夠在平面上畫出,且邊不在非頂點處相交的無向圖。
在平面上畫出的邊不在非頂點處相交的平面圖G的圖形稱為G的平面表示,在平面圖G的一個平面表示中,以G的邊為邊界的連通區域稱為G的該平面表示的面。一個平面圖可以有多個不同的平面表示,但其任何平面表示的面的數目均一樣,這可以用著名的歐拉公式進行計算。若n階平面圖G有m條邊和k個分支,則G的一個平面表示的面數f=m-n+k+1,在無向圖G的任一條邊e上插入一個度為2的頂點,將e一分為二,或者從G中刪去一個度為2的頂點 v,將與v關聯的兩條邊合二為一,可得到圖G′,此時稱G與G′同胚。波蘭數學家Kuratowski給出了判斷一個圖是否為平面圖的準則,即著名的庫拉托夫斯基定理:無向圖G是平面圖當且僅當G沒有同胚於圖1或圖2的子圖(參見圖論)。
給定平面圖G的一個平面表示,在其每個面內找一頂點,若兩個面有m條公共邊,則用m條線連接這兩個面內取定的頂點,並使其分別與m條公共邊相交,由這些頂點和連線組成了邊不在非頂點處相交的圖形,稱以該圖形為其平面表示的平面圖為G的對偶圖。
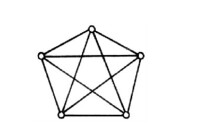
圖1
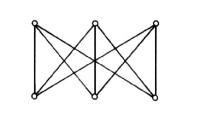
圖2
雖然地球表面是個曲面,但在極小的範圍內,可以把它當做平面,因為地面實形和圖上實形間的誤差已經非
平面圖一個圖能畫在平面上,除結點之外,再沒有邊與邊相交面、邊界和面的次數由連通平面圖G的邊圍成的其內部不含G的結點和邊的區域是面,常用r表示.圍成面的各邊組成的迴路是邊界。邊界迴路的長度是面的次數,記作deg(r).
平面圖定義:將地面上各種地物的平面位置按一定比例尺、用規定的符號縮繪在圖紙上,並注有代表性的高程點的這種圖。
建築平面圖簡稱平面圖,是建築施工中比較重要的基本圖。平面圖是建築物各層的水平剖切圖,假想通過一棟房屋的門窗洞口水平剖開(移走房屋的上半部分),將切面以下部分向下投影,所得的水平剖面圖,就稱平面圖。
建築平面圖既表示建築物在水平方向各部分之間的組合關係,又反映各建築空間與圍合它們的垂直構件之間的相關關係。
在圖論中,平面圖是可以畫在平面上並且使得不同的邊可以互不交疊的圖。而如果一個圖無論怎樣都無法畫在平面上,並使得不同的邊互不交疊,那麼這樣的圖不是平面圖,或者稱為非平面圖。完全圖K5和完全二分圖K3,3是最“小”的非平面圖。
波蘭數學家卡齊米日·庫拉托夫斯基提出的一類禁忌準則(指滿足某種條件的圖就一定無法具有某個性質)中,也包括了平面圖的情況。他提出的一個定理說明:
一個有限圖(頂點數和邊數有限的圖)是平面圖當且僅當它並不包含一個是(有五個頂點的完全圖)或(三個頂點的二部圖)的分割的子圖。
其中,一個圖A是另一個圖B的分割是指:A是在B的基礎上,在某些邊的中間加上頂點
這個定理的一般化是羅伯森-西摩定理。
一個平面圖將平面分成若干個互不相通的封閉區域,以及圖的外部的區域。其中,圖的外面的區域稱為圖的外部面,而圖裡面每個被頂點和邊分割出來的封閉並連通的區域稱為圖的內部面。圍成每個面圖的每個面至少對應著三條邊。
平面圖的頂點個數、邊數和面的個數之間有一個以大數學家萊昂哈德·歐拉命名的公式:
V-E+F=C+1
其中,V是頂點的數目,E是邊的數目,F是面的數目,C是組成圖形的連通部分的數目。當圖是單連通圖的時候,公式簡化為:
V-E+F=2
