傾斜度
指物體或斜面傾斜
傾斜度,是指物體或斜面傾斜、歪斜的程度,與地面的夾角。
釋義
指物體或斜面傾斜、歪斜的程度,與地面的夾角。
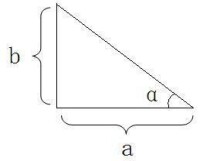
如角α的傾斜度tanα=b:a
傾斜度是表示零件上兩要素相對方向保持任意給定角度的正確狀況。
傾斜度公差是:被測要素的實際方向,對於基準成任意給定角度的理想方向之間所允許的最大變動量。
傾斜度(∠)用來控制零件上被測要素(平面或直線)相對於基準要素(平面或直線)的方向偏離某一給定角度(0°~90°)的程度,即要求被測要素對基準成一定角度(除90°外)。
函數功能
計算數值梯度。
函數F(x,y,...)在(x0,y0,...)的梯度就是函數在該點的導數,通常在數學上記作▽F(x0,y0,...)或gradF(x0,y0,...)。
梯度是一個向量,它的方向是函數在一點變化率最快的方向,而它的模樣就是函數沿這個方向的變化率。
在MATLAB中利用gradient計算梯度,將得到若干向量,它們指出了F的值增大的方向。
語法格式
FX=gradient(F)
其中F是一個向量。該格式返回F的一維數值梯度。FX即∂F/∂x,即沿著x軸(水平軸)方向的導數。
[FX,FY]=gradient(F)
其中F是一個矩陣。該調用返回二維數值梯度的x、y部分。FX對應∂F/∂x,FY對應於∂F/∂y。
[FX,FY,FZ,...]=gradient(F)
這裡,F是一個含有N個自變數的多元函數。
[...]=gradient(F,h)
這裡的h指定了沿著梯度的方向取點的間隔。
[...]=gradient(F,h1,h2,...)
以x,y方向分別為間隔0.2求取矩陣Z的數值梯度,dZ/dx和dZ/dy分別返回到DX,DY中。