共找到13條詞條名為三叉戟的結果展開

三叉戟

數學曲線名稱

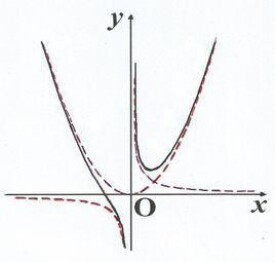
函數y徠=ax²+b/x（a>0，b>0）的圖像稱為三叉戟曲線。

三叉戟是希臘神話中海神波塞冬的武器，而函數y=ax²+b/x的圖像恰如其形，因而得名。牛頓最早研究了這個函數的圖像，所以也稱它為牛頓三叉戟。

目錄

1介紹 2性質漸近線

單調性最小值 3初等證明單調性

最小值 4其它各種符號 5舉例

介紹

函數（）的圖像稱為牛頓三叉戟曲線，也稱其為牛頓三叉戟。

三叉戟[數學曲線名稱]

三叉戟[數學曲線名稱]

函數（）的圖像很像希臘神話中海神波塞冬的武器三叉戟，而牛頓最早研究了這個函數的圖形從而有了牛頓三叉戟的名稱。

性質

漸近線

三叉戟[數學曲線名稱]

（1）因為 →0時 → ，所以牛頓三叉戟有一條鉛直漸近線。

（2）牛頓三叉戟還有兩條曲線漸近線

（I） →0時，牛頓三叉戟有雙曲線漸近曲線；

三叉戟[數學曲線名稱]

（II） → 時，牛頓三叉戟有拋物線漸近曲線。

單調性

函數（）在區間（）、（）上單調遞減；而在區間（）上單調遞增。

最小值

函數（）在區間（）上有最小值。

初等證明

單調性

當時，、，所以，可知函數（）在區間（）上單調遞減；

當時，，所以函數（）在區間（ ]上單調遞減；

當時，，所以函數（）在區間[ ）上單調遞增。

最小值

利用上述單調性，即可知函數（）在區間（）上有最小值。

也可以不依賴於單調性，而直接利用均值不等式來證明：

，等號在時成立。

即當時，函數在區間（）上有最小值。

其它各種符號

在徠其它各種符號下三叉戟的圖形

三叉戟[數學曲線名稱]

三叉戟[數學曲線名稱]

三叉戟[數學曲線名稱]

三叉戟[數學曲線名稱]

三叉戟[數學曲線名稱]

三叉戟[數學曲線名稱]

舉例

上海2007年高考數學試卷第19題：就是一個牛頓三叉戟問題。

已知函數，

（1）判斷的奇偶性；

三叉戟[數學曲線名稱]

（2）若在[2，）上是增函數，求實數的範圍。

【解】（1）當時，是偶函數；當時，既不是奇函數，也不是偶函數。

（2）當時，在(0，）上是增函數，一定也在[2，）上是增函數；

當時，是(0，）上的增函數，一定也是[2，）上的增函數；

三叉戟[數學曲線名稱]

當時，的單調增加區間為 [ ，），據題意有 [ ，），得。

三叉戟[數學曲線名稱]

綜合起來可得實數的範圍是( ，16]。

目錄